2) Partial integro-differential equation
偏积分微分方程
1.
Stability of spatial half discretization for a partial integro-differential equation with a weakly singular kernel;
一类带弱奇异核的偏积分微分方程空间半离散的稳定性
2.
Stability of second order backward difference for a partial integro-differential equation with a weakly singular kernel
一类带弱奇异核的偏积分微分方程二阶向后差分格式的稳定性
3.
In this paper, the second order fully discrete difference method for a partial integro-differential equation is considered.
本文给出了数值求解一类偏积分微分方程的二阶差分全离散格式。
3) integro-partial differential equation
积分-偏微分方程
4) integro-partial differential equation
积分偏微分方程
1.
Memory term and initial boundary value problem in a category of integro-partial differential equations is researched.
考虑带有记忆项的一类积分偏微分方程的初边值问题,采用积分方程理论及Faedo-Galerkin方法,通过积分估计证明了此类方程的初边值问题正则解的存在性。
6) integro-differential equation method
积-微分方程方法
补充资料：偏微分方程
| 偏微分方程 partial differential equation 含有未知函数及其各阶偏导数的方程。如( 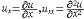 余类此）ut－a2（uxx＋uyy＋uzz）＝0（1）其中u＝u（x，y，z，t）为未知函数，x，y，z，t是自变量。18世纪，数学家们已开始用偏微分方程来研究问题。方程（1）便是用来描述热的传导规律的。1746年，J.LeR.达朗贝尔给出了一维波动方程（两端固定的弦的振动问题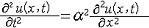）：  由于弦的两端固定，故在x＝0和x＝l处（l为弦的长度）应满足边界条件：u（0，t）＝0 u（l，t）＝0 t≥0（3）又当t＝0时的状态，即初始条件是 u（0，x）＝j（x） ut（0，x）＝ψ（x）（4） 一般，每个偏微分方程有许多解，且含有任意函数，一阶方程的解含有一个任意函数，二阶方程的解含有两个任意函数，例如（2）有解u＝f（x－at）＋g（x＋at），其中f（x）、g（η）是二次可微的函数。通常，更注重求满足某些附加条件的特解：未知函数在初始时刻所满足的条件叫初始条件 ，如（4），在所给区域边界上所满足的条件叫边界条件，如（3），初始条件和边界条件统称定解条件，这都要由实际问题来确定。求方程满足初始条件的定解问题叫初值问题或柯西问题，只含边界条件的定解问题叫边值问题，既有初始条件，又有边界条件的问题称为初边值问题或混合问题。如果某个解，当定解条件中的量变化不大时，解的变化也不大，就称解连续依赖于定解条件。若定解问题的解存在、唯一且连续依赖于定解条件，就称定解问题为适定的或称问题的提法是正确的。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条