1) quasi-linear parabolic integro-differential equations


拟线性抛物型积分微分方程
1.
For quasi-linear parabolic integro-differential equations,.


对于拟线性抛物型积分微分方程,同样采用线性化的方法,利用原问题和线性化问题的等价性,证明了在hp-时间间断Galerkin有限元方法下,拟线性抛物型积分微分方程的有限元解的存在唯一性,又对此近似解做出了L_2模误差估计。
2) nonlinear parabolic integro-differential equations


非线性抛物型偏积分微分方程
3) linear integro-differential equations of parabolic


线性抛物型积分微分方程
1.
In this paper , we consider mixed finit element methods for the initial-boundary value problems of two order hyperbolic equations and linear integro-differential equations of parabolic type , obtain the error estimates of the discrete schemes for this two kinds of problems .
本文讨论了二阶双曲方程和线性抛物型积分微分方程方程初边值问题的混合有限元方法,得到了这两类问题混合有限元离散格式的误差估计。
6) parabolic integro-differential equation


抛物型积分微分方程
1.
This thesis is devoted to the problems of anisotropic finite elements convergence of vicoelastic equation and parabolic integro-differential equation and the error estimates of variable coefficient parabolic equation with anisotropic moving grids finite element methods mainly.
本文主要研究了各向异性网格下粘弹性方程和抛物型积分微分方程的收敛性问题以及各向异性网格下变系数抛物型方程变网格有限元法的误差阶估计问题,全文共由六章组成: 第一章主要对各向异性有限元的研究现状进行了概述,并将本文所做的工作进行了简单介绍。
2.
The discontinuous space-time finite element methods ,that is, approximating functions is discontinuous at the nodes of partition in time, is considered for a parabolic integro-differential equations ,and the theo.
本文利用间断时空有限元方法,即允许近似函数在节点处是间断的,研究了抛物型积分微分方程。
3.
In this paper , we consider the Expanded Mixed Finite Element Method and mixed covolume method for the quasilinear parabolic integro-differential equation and quasilinear parabolic problem.
本文中我们采用扩展混合有限元方法和混合体积元方法数值模拟了二阶拟线性抛物型积分微分方程和二阶拟线性抛物问题。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 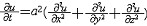 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式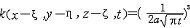 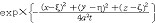 热传导方程初值问题的解可用基本解叠加而成,即 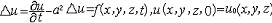 的解为 的解为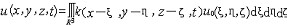 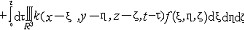 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 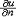 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条