专业词汇(按中图法分类)
1) price Reyleigh equation
物价瑞利方程
1.
This paper studies the Hopf bifurcation diagram and the sufficient criteria that a nonconstantperiodic solutions exist of the price Reyleigh equation with delay.
本文主要研究了具时滞的物价瑞利方程的 Hopf 分支及大范围周期解产生的充分条件。
2.
This paper deals with the dynamical properties of the Hopf bifurcation diagram of the price Reyleigh equation model with delay,and the stability of equilibrium point and the existence of Hopf bifurcation by the method of τ-D partitioning approach of exponential polynomial.
研究具时滞物价瑞利方程模型的动力学性质,利用指数多项式的-τD划分讨论平衡点的稳定性和Hopf分支的存在性,利用具有限时滞Liénard方程的Hopf分支公式获得了Hopf分支方向和周期解的稳定性计算公式,并给出了在r-γ参数平面上的Hopf分支图,得到了"时滞反映出价格对供给具有滞后作用"的结论,合理地解释了经济生活中的价格振荡现象。
2) Rayleihg method
瑞利方法
3) Formula of Riccati
瑞卡提方程
4) arrhenius equation
阿瑞尼氏方程式
5) virial eguation
维利方程
6) Pauli equation
泡利方程
1.
Considering the coordinates-coordinates′ non-commutation,from Moyal-Weyl multiplication and Bopp shift,the Pauli equation in non-commutative space are given by using the algebra relation in quantum mechanics.
本文从Moyal-Weyl乘法出发,考虑了坐标-坐标的非对易性,利用非对易空间量子力学的代数关系(Bopp变换),给出了非对易空间中的泡利方程。
补充资料：伯努利方程
| 伯努利方程 Bernoulli's equation 理想正压流体在有势彻体力作用下作定常运动时，运动方程（即欧拉方程）沿流线积分而得到的表达运动流体机械能守恒的方程。因D.伯努利于1738年提出而得名。对于重力场中的不可压缩均质流体 ，方程为 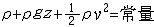 ，式中p、ρ、v 分别为流体的压强、密度和速度；z为铅垂高度；g为重力加速度。 上式各项分别表示单位体积流体的压力能p、重力势能ρg z和动能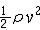 ，在沿流线运动过程中，总和保持不变，即总能量守恒。但各流线之间总能量（即上式中的常量值）可能不同。对于气体，可忽略重力，方程简化为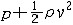 ＝常量(p0)，各项分别称为静压、动压和总压。显然 ，流动中速度增大，压强就减小；速度减小， 压强就增大；速度降为零，压强就达到最大(理论上应等于总压)。飞机机翼产生举力，就在于下翼面速度低而压强大，上翼面速度高而压强小 ，因而合力向上。 据此方程，测量流体的总压、静压即可求得速度，成为皮托管测速的原理。在无旋流动中，也可利用无旋条件积分欧拉方程而得到相同的结果但涵义不同，此时公式中的常量在全流场不变，表示各流线上流体有相同的总能量，方程适用于全流场任意两点之间。在粘性流动中，粘性摩擦力消耗机械能而产生热，机械能不守恒，推广使用伯努利方程时，应加进机械能损失项。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条
