1) m-th order total differential
m阶全微分
2) m-th order differentiable
m阶可微
3) n-order m-dehree homogeneous differential equations
n阶m次微分方程
4) order m complete graph Km
m阶完全图K_m
5) complet second order linear differential equation
完全二阶线性微分方程
6) Integral Operator
m阶积分算子
补充资料：全微分
| 全微分 complete differential 如果二元函数z＝f(x，y)在P(x，y)点的增量Δz＝f(x＋Δx，y＋Δy)－f(x，y) 能表示为Δz＝AΔx＋BΔy＋0(ρ)，其中 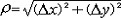 ，A、B，是与Δx和Δy无关的常数，0（ρ）表示当ρ→0时比ρ高阶的无穷小量， 即0(ρ)趋于0的速度比ρ趋于0的速度要快，AΔx＋BΔy成为函数增量的主要部分，并且关于Δx、Δy是线性的，则说二元函数z＝f（x，y)Ｔ赑点可微，称AΔx＋BΔy为函数的全微分。记为dz＝AΔx＋BΔy，因自变量的微分等于改变量，所以dz＝Adx＋Bdy。与一元函数所不同之处是，在一元函数中，函数在P点可微与可导是等价的，但对二元函数来说，由可微可推出两个偏导数(见偏导数)存在，但光从两个偏导数存在还不能得出可微的结论。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条