1) tlarmonic Bloch functionS


调和的Bloch函数
2) harmonic α-Bloch function


调和α-Bloch函数
1.
In this paper,characterizations of harmonic α-Bloch function and harmonic little α-Bloch function are given by means of increasing functions,which extends earlier results of the second author.
用给定的增函数刻画调和α-Bloch函数和调和小α-Bloch函数的特征,它们改进了第二作者早期的一些结果。
3) harmonic little α-Bloch function


调和小α-Bloch函数
1.
Harmonic α-Bloch and harmonic little α-Bloch functions;


调和α-Bloch函数和调和小α-Bloch函数
4) Bloch functions


Bloch函数
1.
In this paper, we obtain a series of characterizations of Bloch functions defined on the unit ball B of Cn by using the fractional derivative, the multipliers Jβ and Dβ, and the generalized Carleson measure on B, which generalizes the known results in the case of one complex variables.
以C~n中单位球B上全纯函数的分数次导数和系数乘子变换J~β、D~β以及B上的广义Carleson测度对Bloch函数进行了研究,得到了B上Bloch函数的一系列等价特征,推广了在单复变情形已有的工作,对little Bloch函数也进行了相应的研究。
2.
We gave several distance formulas from Bloch functions to some Q_K-type spaces,which generalize distance formulas from Bloch functions to BMOA space by Jones and to some M(o|¨)bius invariant spaces by Ruhan Zhao.
Jones用Carleson测度刻划出了Bloch函数到BMOA空间的距离,赵如汉给出Jones的一个推广定理,得到Bloch函数到一些M(o|¨)bius不变函数空间的距离。
5) Bloch function


Bloch函数
1.
A generalization of a criterion of Bloch functions and little Bloch functions;


Bloch函数和小Bloch函数判别准则的推广(英文)
2.
Mbius invariant gradient and α-Bloch functions.;


Mobius不变梯度和α-Bloch函数
3.
Weighted characterization of Bloch function in the unit ball of C~n;


单位球上Bloch函数的带权特征
6) little Bloch function


小Bloch函数
1.
A generalization of a criterion of Bloch functions and little Bloch functions;


Bloch函数和小Bloch函数判别准则的推广(英文)
补充资料:调和函数
| 调和函数 harmonic function 在平面区域D上定义的函数u=u( x,y),若有二阶连续偏导数,且满足二阶拉普拉斯方程 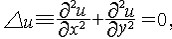 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有 则称u=u(x,y)为D上的调和函数。调和函数与解析函数有密切关系 ,在平面区域D上的解析函数的实部与虚部都是调和函数,由于这一对调和函数还满足柯西黎曼条件,因而特别称虚部是实部的共轭调和函数。反之一个单连域上的调和函数一定可以是一个单值解析函数的实部,而且这样的解析函数不唯一,它们相互之间可以相差一个纯虚数,而在多连通区域上,一个调和函数一般是一个多值解析函数的实部。u(x,y)是区域D上调和函数的充要条件是u(x,y)在区域D连续且对D内任意一点P(x,y),存在正实数rp,对所有正数r<rp有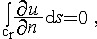 其中cr是以 P(x,y)为心,r为半径的圆, 其中cr是以 P(x,y)为心,r为半径的圆,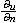 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在 是u(x,y)沿cr法向的导数,当u(x,y)是一个圆盘△上的调和函数,且在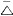 上连续时,则u(x,y)在D内任一点的值可表为积分公式: 上连续时,则u(x,y)在D内任一点的值可表为积分公式: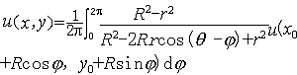
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |