1) factorization of function


亚纯函数的分解
3) neighborhoods of meromorphic functions


亚纯函数的邻域
5) Meromorphic function


亚纯函数
1.
On an uniqueness of meromorphic functions sharing two finite sets;


关于分担两个集合的亚纯函数的唯一性
2.
Uniqueness of meromorphic functions concerning weakly weighted-sharing small functions;


涉及权弱分担小函数的亚纯函数唯一性
3.
Uniqueness theorem of meromorphic functions sharing one value;


权分担一个值的亚纯函数的唯一性定理
6) meromorphic
[,merə'mɔ:fik]


亚纯函数
1.
The problem of uniqueness of meromorphic functions is discussed.


讨论了亚纯函数的惟一性问题,证明存在一个具有12个元素的集合S使得对任意2个非常数的亚纯函数f与g,只要满足3)(S,f)=3)(S,g)和({∞},f)=({∞},g),必有f≡g。
2.
We will give reduce demonstration for a lemma in four values theorem of meromorphic function.
给出了亚纯函数四值定理中一个引理的简化证明。
3.
In this paper we get the following results: Let (z) be a meromorphic function in domain G which is not identically zero, a1(z), a2(z), …,ak(z) be holomorphic function in domain G, F={f} be a family of meromorphic functions in G.
本文获得如下结果:设(z)为区域G内一不恒为零的亚纯函数,a1(z),a2(z),…,ak(z)为区域G内的全纯函数,F={f}为G内一亚纯函数族。
补充资料:亚纯函数
| 亚纯函数 meromorphic function 在区域D上有定义 ,且除去极点之外处处解析的函数。比如有理函数就是在扩充复平面上的亚纯函数,它是两个多项式的商 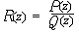 ,而Q(z)的零点是R(z)的极点 ,即R(z)有有限多个极点,∞点是R(z)的极点或可去奇点 。复平面上不是有理函数的亚纯函数称为超越亚纯函数。例如ctgz就是超越亚纯函数 ,它以kπ为全部极点 ,超越亚纯函数一定有无限多个极点。有理函数可以分为部分分式,即 
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |