1) meromorphic function element


亚纯函数元
2) meromorphic function element


亚纯函数元素
3) Meromorphic function


亚纯函数
1.
On an uniqueness of meromorphic functions sharing two finite sets;


关于分担两个集合的亚纯函数的唯一性
2.
Uniqueness of meromorphic functions concerning weakly weighted-sharing small functions;


涉及权弱分担小函数的亚纯函数唯一性
3.
Uniqueness theorem of meromorphic functions sharing one value;


权分担一个值的亚纯函数的唯一性定理
4) meromorphic
[,merə'mɔ:fik]


亚纯函数
1.
The problem of uniqueness of meromorphic functions is discussed.


讨论了亚纯函数的惟一性问题,证明存在一个具有12个元素的集合S使得对任意2个非常数的亚纯函数f与g,只要满足3)(S,f)=3)(S,g)和({∞},f)=({∞},g),必有f≡g。
2.
We will give reduce demonstration for a lemma in four values theorem of meromorphic function.
给出了亚纯函数四值定理中一个引理的简化证明。
3.
In this paper we get the following results: Let (z) be a meromorphic function in domain G which is not identically zero, a1(z), a2(z), …,ak(z) be holomorphic function in domain G, F={f} be a family of meromorphic functions in G.
本文获得如下结果:设(z)为区域G内一不恒为零的亚纯函数,a1(z),a2(z),…,ak(z)为区域G内的全纯函数,F={f}为G内一亚纯函数族。
5) mermorphic function


亚纯函数
1.
Normal families of mermorphic function concerning differential monomials


涉及微分多项式的亚纯函数的正规族
2.
In this dissertation, we study normal families of mermorphic functions, which is an important subject in complex analysis.
本文主要研究亚纯函数族的正规性问题。
6) meromophic function


亚纯函数
1.
There is only one Borel exceptional value at most, when the series beyond meromophic function is below 1.
证明了当超越亚纯函数的级小于1时,其Borel例外值最多只有一个。
2.
It put much emphasis on the discussion of the uniquenss of some meromophic functions which can meet the demand of some defetive value conditions,and obtain a series of interesting results, which at the same time answer one question put forward by Yi Hongxun and C.
应用Nevanlinna理论讨论满足一些亏值条件的亚纯函数的唯一性问题,得到一系列结果,同时回答了仪洪勋和杨重骏提出的问题。
3.
The normality of meromophic functions with shared values is dealt with and the following result is achieved.
研究一类亚纯函数族在分担值条件下的正规性。
补充资料:亚纯函数
| 亚纯函数 meromorphic function 在区域D上有定义 ,且除去极点之外处处解析的函数。比如有理函数就是在扩充复平面上的亚纯函数,它是两个多项式的商 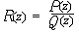 ,而Q(z)的零点是R(z)的极点 ,即R(z)有有限多个极点,∞点是R(z)的极点或可去奇点 。复平面上不是有理函数的亚纯函数称为超越亚纯函数。例如ctgz就是超越亚纯函数 ,它以kπ为全部极点 ,超越亚纯函数一定有无限多个极点。有理函数可以分为部分分式,即 
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |