1) complex function theory


复函数论
1.
In course of the education reform of complex function theory,the author uses the exterior differential tools shortly to prove well—known Cauchy theorem and formulas.
在复函数论的教学改革中,利用外微分工具简洁地证明了著名的柯西定理和公式。
2) composite number-theorectic functions


复合数论函数
4) Theory of several complex variables


多复变函数论
5) multivariable complex analysis


多复变函数理论
6) complex analysis


复分析,复变函数论
补充资料:数论
| 数论 number,theory of 研究数的规律,特别是研究整数性质的数学分支。它既是最古老的数学分支,又是很活跃的数学研究领域。从方法上来说,数论可分为初等数论、解析数论和代数数论。 对于一个大于1的整数,若它的正因数只有1和它本身,则称这个整数为素数(或质数),否则称为复合数。欧几里得证明过素数有无穷多个。他还证明过每个复合数都可以唯一地表成素数的乘积,这又称为算术基本定理。 数论研究不定方程的求解问题。大约在公元250年, 丢番图研究过这种方程,故又称为丢番图方程。最简单的不定方程是一次不定方程ax+by=1,式中a,b为给定的整数,并且它们互素。借助于辗转相除法可以求出它的解。中国古代已有关于不定方程的研究记载,例如5世纪《张丘建算经》中的百鸡问题,还有《孙子算经》中的物不知其数,都属于不定方程问题。又如公元前1100年商高曾给出不定方程。x2+y2=z2的一组x=3,y=4,z=5。这个不定方程有无穷多组整数解。不定方程的研究虽有久远的历史,但完满解决的问题并不多。 数论研究将整数表为某种整数之和的问题,这一数论分支称为堆叠数论。例如每一个不小于4的偶数可以表为两个奇素数之和,这就是尚未解决的哥德巴赫猜想。 特殊类型的整数,是数论最早研究的对象之一。例如形如 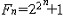 的数,称为费马数。P.de费马猜测,Fn都是素数,但L.欧拉证明了,641整除F5,所以费马猜测被否定了。形如Mp=2p-1(p为素数)的素数称为梅森素数。是否有无穷多个梅森素数是一个至今没有解决的问题。 的数,称为费马数。P.de费马猜测,Fn都是素数,但L.欧拉证明了,641整除F5,所以费马猜测被否定了。形如Mp=2p-1(p为素数)的素数称为梅森素数。是否有无穷多个梅森素数是一个至今没有解决的问题。一般说来,用算术推导方法来论证的数论命题的分支称为初等数论,而解析数论则是把算术问题化为分析问题,然后用分析的成果与方法来处理,从而导出算术的结果。 解析数论开始于L.欧拉的一些研究。其中之一是关于素数有无穷多个的分析证明。令π(x)表示不超过x的素数的个数,关于π(x)的研究是解析数论的中心问题之一。1896年J.阿达马和C.de la瓦莱-普桑同时并相互独立地证明了素数定理,即当x→∞时,π(x)~x/logx。从此解析数论开始得到迅速发展。 解析数论中许多重要问题都同黎曼猜想有关。B.黎曼引进了复变函数ζ(s),通常称为黎曼ζ函数。当复变数s的实部Res=σ>1时,ζ(s)由级数 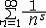 来定义。当σ≤1时,由解析开拓来定义。黎曼猜想是指:在带状区域0≤σ≤1中,ζ(s)的零点都在直线σ=1/2上 。黎曼猜想的解决目前还相差很远。由于素数分布问题同ζ( s)的性质密切相关,因此研究ζ(s)的性质特别是它的零点的性质是非常重要的。黎曼开创了解析数论的新时期。也推动了复变函数的发展。 来定义。当σ≤1时,由解析开拓来定义。黎曼猜想是指:在带状区域0≤σ≤1中,ζ(s)的零点都在直线σ=1/2上 。黎曼猜想的解决目前还相差很远。由于素数分布问题同ζ( s)的性质密切相关,因此研究ζ(s)的性质特别是它的零点的性质是非常重要的。黎曼开创了解析数论的新时期。也推动了复变函数的发展。从数论发展的历史可以看出,不同的研究方法得出不同的结果。以分析问题为例。命P(n)表示将正整数n分拆成整数之和的方法数。用简单的算术方法可以得到P(n)的最粗略估计 : 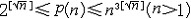 ,用较初等的解析方法可以得出, ,用较初等的解析方法可以得出,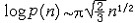 ,用深刻的解析方法可以得出P(n)的渐近公式 ,用更深刻的模形式论的结果及解析方法还可以求出P(n)的展开式。 ,用深刻的解析方法可以得出P(n)的渐近公式 ,用更深刻的模形式论的结果及解析方法还可以求出P(n)的展开式。另一方面,虽然有的问题已经由分析方法解决,但是寻求一个算术的解决方法或较初等的分析解决方法,仍很重要。例如寻求素数定理的初等分析证明,是数论中历时很久的问题之一。这一证明是由 A.塞尔伯格和P.爱尔特希于1949年首先分别给出的。 首项系数为1的整系数方程的根 ,称为代数整数。例如普通整数 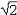 ,i, ,i,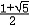 等都是代数整数。代数数论就是研究代数整数性质的一个数论分支。代数数论的重要性不仅在于它是为弄清普通整数的某些性质所不可缺少的,而且还在于它的成果几乎可以用到每一个数学领域中去。 等都是代数整数。代数数论就是研究代数整数性质的一个数论分支。代数数论的重要性不仅在于它是为弄清普通整数的某些性质所不可缺少的,而且还在于它的成果几乎可以用到每一个数学领域中去。30多年来,电子计算机的产生与发展,给科学技术带来无比巨大的变革,这使数论有了非常广泛的直接应用途径。例如近20年来发展起来的高维数值积分的数论网格法的研究中,数论的成果被广泛应用。在编码和数字信号处理中,数论也有很重要的应用。随着科学技术的发展,数论除了它在纯粹数学中的基础性质外,正日益展现出直接应用的途径。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条