1) "weakly integrally small" coefficient


"弱积分小"系数
3) integral coefficient


积分系数
1.
This paper introduces firstly the configuration and operation principle of double close-loop controlled voltage source inverter, then deduces the expression of equivalent output impedance of the inverter through its close-loop transfer function, and finally analyzes the impacts of the proportional and integral coefficients in voltage regulator.
介绍了双闭环控制电压源逆变器的结构和工作原理,利用其闭环传递函数求解出了逆变器等效输出阻抗的表达式,分析了电压外环比例系数、积分系数和电流内环等效放大倍数对逆变器外特性的影响。
4) "Integral small" coefficient


"求积小"系数
5) integral values of wavelet


小波积分数
6) integral weighted coefficients


积分权系数
1.
The paper studys on the calculating fortilulas of the integral weighted coefficients when the duol weigheed function method is used to paranteter estimation witn discrete series.
用双权函数估计不连序系列的统计参数时,积分权系数计算公式的研
补充资料:积分
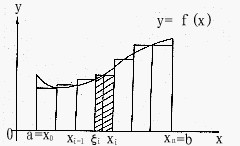
| 积分 integral 从不同的问题抽象出来的两个数学概念。定积分和不定积分的统称。不定积分是为解决求导和微分的逆运算而提出的。例如:已知定义在区间I上的函数f(x),求一条曲线y=F(x),x∈I,使得它在每一点的切线斜率为F′(x)= f(x)。函数f(x)的不定积分是f(x)的全体原函数(见原函数),记作 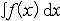 。如果F(x)是f(x)的一个原函数,则 。如果F(x)是f(x)的一个原函数,则 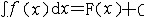 ,其中C为任意常数。例如, ,其中C为任意常数。例如,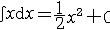 定积分是以平面图形的面积问题引出的。如右上图,y=f(x)为定义在[a,b]上的函数,为求由x=a,x=b ,y=0和y=f(x)所围图形的面积S,采用古希腊人的穷竭法,先在小范围内以直代曲,求出S的近似值,再取极限得到所求面积S,为此,先将[a,b]分成n等分:a=x0<x1<…<xn=b,取ζi∈[xi-1,xi],记Δxi=xi-xi-1, 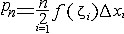 ,则pn为S的近似值,当n→+∞时,pn的极限应可作为面积S。把这一类问题的思想方法抽象出来,便得定积分的概念:对于定义在[a,b]上的函数y=f(x),作分划a=x0<x1<…<xn=b,若存在一个与分划及ζi∈[xi-1,xi]的取法都无关的常数I,使得 ,则pn为S的近似值,当n→+∞时,pn的极限应可作为面积S。把这一类问题的思想方法抽象出来,便得定积分的概念:对于定义在[a,b]上的函数y=f(x),作分划a=x0<x1<…<xn=b,若存在一个与分划及ζi∈[xi-1,xi]的取法都无关的常数I,使得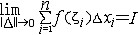 ,其中 ,其中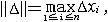 则称I为f(x)在[a,b]上的定积分,表为 则称I为f(x)在[a,b]上的定积分,表为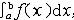 即 即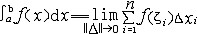 称[a,b]为积分区间,f(x)为被积函数,a,b分别称为积分的上限和下限。当f(x)的原函数存在时,定积分的计算可转化为求f(x)的不定积分: 称[a,b]为积分区间,f(x)为被积函数,a,b分别称为积分的上限和下限。当f(x)的原函数存在时,定积分的计算可转化为求f(x)的不定积分: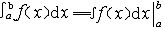 这是牛顿莱布尼兹公式。例如, 这是牛顿莱布尼兹公式。例如,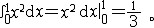
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条