1) (λ,μ)-convex functional


(λ,μ)-凸泛函
2) λ-convex functions


λ-凸函数
3) (λ,μ)-fuzzy convex sublattice


(λ,μ)f-uzzy凸子格
1.
Based on the characterizations of fuzzy(dual) ideal and fuzzy prime ideal and convex sublattice in crisp lattice,some basic properties of L-fuzzy lattice are discussed,and the concepts(λ,μ)-fuzzy sublattice,(λ,μ)-fuzzy ideal(dual ideal) and(λ,μ)-fuzzy convex sublattice are introduced.
基于一般格上模糊(对偶)理想、模糊素理想和凸子格的一些性质,讨论了L-fuzzy格的一些基本性质,并给出了(λ,μ)-fuzzy子格,(λ,μ)-fuzzy理想(对偶理想)和(λ,μ)f-uzzy凸子格概念,建立了(λ,μ)-fuzzy凸子格与其水平子格之间的联系。
4) λ subconvex function


λ-次凸函数
1.
As a generalization of λ-subconvex function,the concept of semilocally λ-subconvexfunction is introduced in this paper.
作为对λ-次凸函数的推广,本文引入了半局部λ-次凸函数概念,初步研究了它的一些等价性质和一些极值性质。
5) subconvex function


次凸泛函
1.
In this paper,making use of hyperplane method,we improve the proof of the separation theorem;On the other hand,we use a new method of moving neighborhood to simplify the proof for the continuity of a subconvex function defined on a convex in a normed linear space.
在巴拿赫空间理论中,Hahn-Banach泛函延拓定理作为泛函分析三大基本定理之一,分隔性定理是Hahn-Banach定理的重要应用,本文利用"超平面"的方法,改进了一个分隔性定理的证明;另外,本文利用邻域的"平移"方法,给出了定义在赋范线性空间内的凸集上的次凸泛函连续性的简捷证明。
6) explicit convex


显凸泛函
1.
In this paper,the concept of explicit convex function is given,then tow sufficient conditions of explicit convex functions are obtained by using G-differentiability of functions in Banach space.
在Banach空间中给出了显凸泛函的概念,然后利用泛函的G-可微性,给出了显凸泛函的两个充分条件。
补充资料:泛函
| 泛函 functional 定义于一般集合,取数值(实数值或复数值)的映射。又称泛函数。是微积分中函数概念的发展和拓广。例如,取非空集X={f:f为定义在[a,b]上的连续函数},映射F:X→R为F(f)= 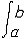 f(x)dx。F就是定义在集合X上的一个泛函。因此,泛函可通俗地看作以函数为自变元的函数,在很多情况下,泛函的定义域均为函数集。泛函概念的产生直接与变分法中的求极值问题有关。上面的例子还具有这样的性质: f(x)dx。F就是定义在集合X上的一个泛函。因此,泛函可通俗地看作以函数为自变元的函数,在很多情况下,泛函的定义域均为函数集。泛函概念的产生直接与变分法中的求极值问题有关。上面的例子还具有这样的性质: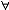 f,g∈X 和 f,g∈X 和 α,β∈R,有以下等式成立:F(αf+βg)= α,β∈R,有以下等式成立:F(αf+βg)= [αf(x)+βg(x)]dx= α [αf(x)+βg(x)]dx= α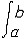 f(x)dx+β f(x)dx+β g(x)dx=αF(f)+βF(g),称这样的泛函为线性泛函。线性泛函是算子理论研究的主要对象之一,也是研究空间性质及结构的重要工具。因为利用线性连续泛函可导出对偶空间(由定义在X上的一切线性连续泛函组成的集合,并赋以自然的加法、数乘运算及范数)的概念,而空间X与其对偶空间 X*间的关系对于认识空间本身的性质和研究算子的性质都起着基础的作用。 g(x)dx=αF(f)+βF(g),称这样的泛函为线性泛函。线性泛函是算子理论研究的主要对象之一,也是研究空间性质及结构的重要工具。因为利用线性连续泛函可导出对偶空间(由定义在X上的一切线性连续泛函组成的集合,并赋以自然的加法、数乘运算及范数)的概念,而空间X与其对偶空间 X*间的关系对于认识空间本身的性质和研究算子的性质都起着基础的作用。除此之外,对应于多线性算子有多重线性泛函概念,例如在希尔伯特空间中,双线性泛函作为表示工具在处理问题时十分方便有效。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条