1) Carleson inequality


Carleson不等式
1.
This paper reaserches Carleson inequality in fraction deritive and its analogue in H P space.
研究了分数次导数情形的 Carleson不等式以及该不等式在 Hp空间上的模
2) Carleson inverse inequality


Carleson逆不等式
1.
Inequality to describe double Carleson measure and description of Carleson inverse inequality;
双Carleson测度的积分不等式及对Carleson逆不等式的刻画
3) inequality
[英][,ɪnɪ'kwɔləti] [美]['ɪnɪ'kwɑlətɪ]


不等式;不等
4) isoperimetric inequality


等周不等式
1.
The isoperimetric inequality on the Heisenberg group H~n;


关于Heisenberg群上的等周不等式
2.
We will derive the plane isoperimetric inequality and the Bonnesen s isoperi- metric inequality by the method of integral geometry.
将用积分几何方法给出平面等周不等式以及Bonnesen型不等式,平面区域D的面积、周长、最大内接园半径及最小外接园半径的一些几何不等式的简单证明。
5) equivalent inequality


等价不等式
6) Isodiametric inequalities


等径不等式
补充资料:不等式
| 不等式 inequality 用不等号将两个解析式连结起来所成的式子。例如x2+y2≥2xy,sinx≤1,ex>0 ,2x<3等 。根据解析式的分类也可对不等式分类,不等号两边的解析式都是代数式的不等式,称为代数不等式;只要有一边是超越式,就称为超越不等式。例如 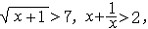 是代数不等式,lg(1+x)>x是超越不等式。 是代数不等式,lg(1+x)>x是超越不等式。通常不等式中的数是实数,字母也代表实数,不等式的一般形式为F(x,y,……,z)≤G(x,y,……,z )(其中不等号也可以为<,≥,> 中某一个),两边的解析式的公共定义域称为不等式的定义域,不等式既可以表达一个命题,也可以表示一个问题。例如,平均值不等式定理“x1,x2,……,xn取任意正数时,不等关系 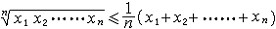
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |