1) Cauchy-Buniakowski inequality


Cauchy-Buniakowski不等式
2) Buniakowski-Cauchy inequality


Buniakowski-Cauchy不等式
1.
On the basis of analyzing and studying Buniakowski-Cauchy inequality,a new strengthened popularization of Buniakowski-Cauchy inequality s infinite sum is obtained.
在分析研究Buniakowski-Cauchy不等式的基础上,得到了此不等式的无限可和性的新加强推广形式,并给出了十分简洁有趣的构造性方法的证明。
3) Buniakowski-Cauchy integral inequality


Buniakowski-Cauchy积分不等式
1.
New popularization and application of Buniakowski-Cauchy integral inequality;


Buniakowski-Cauchy积分不等式的新推广
5) Buniakowski-Schwarz inequality


Buniakowski-Schwarz不等式
1.
On the basis of research results, popularization of Buniakowski-Schwarz inequality in L pspace is discussed, and a new thinking and method are provided for further studying integral theory in L pfunction space.
现在已有研究成果的基础上,讨论了Buniakowski-Schwarz不等式在Lp空间中的推广形式,为进一步研究Lp函数空间的积分理论提供一种新的思想和方法。
6) Cauchy inequality


Cauchy不等式
1.
On the equivalence of the Hoder inequality and the Cauchy inequality;


Hoder不等式与Cauchy不等式的等价性
2.
Generalizations of Cauchy inequality about matrix versions;


Cauchy不等式矩阵形式的推广
3.
Cauchy inequality is very important and widely u sed in inequality studies.


Cauchy不等式在不等式研究中有着重要的地位和广泛的应用。
补充资料:不等式
| 不等式 inequality 用不等号将两个解析式连结起来所成的式子。例如x2+y2≥2xy,sinx≤1,ex>0 ,2x<3等 。根据解析式的分类也可对不等式分类,不等号两边的解析式都是代数式的不等式,称为代数不等式;只要有一边是超越式,就称为超越不等式。例如 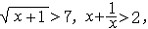 是代数不等式,lg(1+x)>x是超越不等式。 是代数不等式,lg(1+x)>x是超越不等式。通常不等式中的数是实数,字母也代表实数,不等式的一般形式为F(x,y,……,z)≤G(x,y,……,z )(其中不等号也可以为<,≥,> 中某一个),两边的解析式的公共定义域称为不等式的定义域,不等式既可以表达一个命题,也可以表示一个问题。例如,平均值不等式定理“x1,x2,……,xn取任意正数时,不等关系 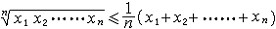
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|
|
| ©2011 dictall.com | |