1) Parabolic equation with variable coefficient


变系数抛物方程
2) variable coefficient parabolic equation


变系数抛物型方程
1.
By supposing the soultion of the type of Fourier series,we obtain the approximate solutions for the double?moving boundary problems of a variable coefficient parabolic equation.
通过构造Fourier型级数解 ,给出一类变系数抛物型方程双移动边界问题的求解方
4) parabolic equation


抛物方程
1.
Application of the wide-angle parabolic equation under impedance boundary condition;


宽角抛物方程在阻抗边界条件下的应用
2.
Blow-up of nonnegative radial solutions for a family of parabolic equations in bounded domain in RN;
R~N中有界域上的一类抛物方程非负径向解的爆破问题
3.
Renormalized solutions of a class of strongly degenerate quasilinear parabolic equations;


一类强退化拟线性抛物方程的重整化解
5) parabolic equations


抛物方程
1.
Constructive method for the Cauchy problem of parabolic equations and its mechanization;


抛物方程柯西问题的构造解法及机械化求解
2.
An alternating group method for four order parabolic equations;


四阶抛物方程的一类交替分组方法
3.
In this paper the oscillation property of a class of nonlinear parabolic equations with several delays is discussed.
研究了一类非线性时滞抛物方程在两类齐次边界条件下解的振动性质,获得了判别其所有解振动的充要条件,并通过实例对主要结果进行阐明。
6) variable coefficient equation


变系数方程
1.
Considering the(2+1) dimensional variable coefficient equation,doing some unknown functions transformation for seed solutions of the equation,we make full use of Backlund transformation and performing mathematical calculations to obtain a series of exact solutions,in which some solution contains arbitrary functions.
考虑一般的变系数方程,对方程的种子解作适当的未知函数变换,然后利用backlund变换通过演算获得(2+1)维变系数方程的一系列精确解,其中有的解中含有任意函数,当这些任意函数取某些特殊函数时,这些解具有丰富的结构。
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 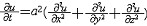 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式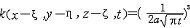 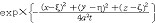 热传导方程初值问题的解可用基本解叠加而成,即 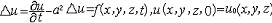 的解为 的解为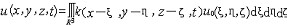 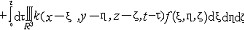 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 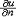 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条