4) parabolic partial differential equation


抛物型偏微分方程
1.
The models of American option and perpetual American option are a free boundary problem of parabolic partial differential equation and ordinary differential equation respectively.
在相应的基本假设下,美式期权的定价模型是一个抛物型偏微分方程自由边界问题,而永久美式期权的定价模型是一个常微分方程自由边界问题。
2.
With the function approximation and Tikhonov regularization as the base,this paper presents a new type of iterative algorithm to solve inverse problems of parameter identification for onedimension parabolic partial differential equations.
以函数逼近和Tikhonov正则化为基础,利用算子识别摄动法和线性化技术提出求解一维抛物型偏微分方程参数识别反问题的迭代算法,拓宽了求解此类反问题泛定方程和初边值条件的适用范围。
3.
In this paper, the oscillation for a class of impulsive neutral parabolic partial differential equations is investigated.
研究一类脉冲中立抛物型偏微分方程的振动性,借助Green散度定理和脉冲中立型微分方程,得到了该类方程在Dirichlet边界条件下所有解振动的一个充要条件。
5) two-dimensional parabolic partial differential equation


二维抛物型偏微分方程
6) multi-dimensional bolic parabolic type partial differential equation


多维抛物型偏微分方程
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 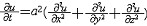 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式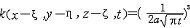 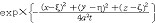 热传导方程初值问题的解可用基本解叠加而成,即 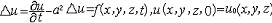 的解为 的解为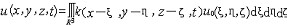 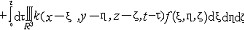 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 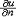 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条