1) Degenerate parabolic systems


退缩抛物方程组
1.
A class degenerate parabolic systems is considered.


讨论一类退缩抛物方程组的局部存在性与爆破性,证明在一定条件下解在有限时刻爆破,给出爆破时间的一个上限估计。
2) degenerate parabolic equation


退缩抛物型方程
1.
Quenching for singular and degenerate parabolic equation;


含奇异项的退缩抛物型方程解的猝灭现象
2.
The relation about the existence of solution and initial condition for Cauchy problem of a singular and degenerate parabolic equation is considered.
考虑了含奇异项的退缩抛物型方程柯西问题解的存在性与初始条件的关系 ,证明了在初值较小时解是全局存在的 ,在初值较大时解会在有限时刻产生猝灭现
3.
The existence and blow-up of a class degenerate parabolic equation on semi-infinite space is considered.
讨论半无界空间上退缩抛物型方程解的存在性与爆破性质。
4) degenerate parabolic system


退化抛物方程组
1.
Global existence and blow-up of solutions to quasilinear degenerate parabolic system;


拟线性退化抛物方程组解的整体存在和有限爆破
2.
This paper deals with a degenerate parabolic system with nonlocal sources.


本文讨论一类具有非局部源退化抛物方程组。
3.
this paper investigates the uniquenes S Of solutions with compact support of a boundary value problem which comes from t He study of asymptotic behavior of blow up solution of the degenerate parabolic System.
研究一个来源于研究退化抛物方程组的渐近性而产生的常微分方程组 。
6) doubly degenerate parabolic equation


双重退缩抛物方程
1.
In this paper,we study the Cauchy problem with initial datum u(x,0)=μ∈L ∞ loc (R N) for the nonlinear doubly degenerate parabolic equation with asborption u t=div(|u m| p-2 u m)-u q .
讨论带吸收项的非线性双重退缩抛物方程ut =div(| um|p-2 um) -uq 具有初值u(x ,0 ) =μ∈L∞loc(RN)的Cauchy问题 。
2.
This paper deals with the extinction properties of solutions of the first initial-boundary value problem for the nonlinear doubly degenerate parabolic equation.
研究非线性双重退缩抛物方程第一初边值问题解的耗竭性 ,应用能量方法 ,对具零Dirichlet边界条件和非负初值的方程 ,给出了解在有限时间内耗竭的充分条件 ,从而推广了Tsutsu miM等人的结
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 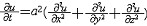 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式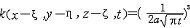 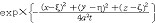 热传导方程初值问题的解可用基本解叠加而成,即 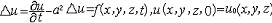 的解为 的解为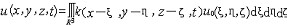 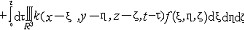 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 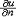 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条