1) theorem of equipartition of energy
能均分定理
1.
Review"Demonstration of the theorem of equipartition of energy on rotation and vibration with the extension of Maxwell velocity distribution law";
也谈转动和振动的概率分布与能均分定理的证明
2.
Demonstration of the theorem of equipartition of energy on rotation and vibration with the extension of Maxwell velocity distribution law;
用推广的Maxwell速度分布律证明转动、振动方式能均分定理
3) principle of equipartition of energy
能量均分原理
1.
The rate equation of solute migration was derived from Maxwell distribution of energy and the principle of equipartition of energy.
以麦克斯韦能量分布和能量均分原理建立溶质迁移速度方程;用迁移活化能解释溶质保留时间;尝试从动力学观点探讨色谱过程机理。
4) value distribution theorem
均值分布定理
5) mean value theorem
均值定理
1.
Two new interesting arithmetical functions are introduced in this paper,and by using the mean value theorems of the Dirichlet L-functions and the properties of primitive character,some sharper asymptotic formulae are obtained.
Lehmer问题有关的两个求和估计问题,并利用特征的正交关系,将其转化为有关Gauss和及Dirichlet L-函数的求和式,同时结合原特征的性质与L-函数的均值定理得到两个有趣的渐近公式,表明所研究的数论函数具有较好的渐近分布性质。
2.
Results The value distribution properties of this function were solved and an interesting mean value theorem was obtained.
结果关于这个函数的值分布性质,给出了一个有趣的均值定理。
6) mean value
均值定理
1.
The main purpose of this paper is using the mean theorem of Dirichlet L-functions to study a sum analogous to the Dedekind sum and its 1/2 power mean value formula and give a sharper power mean formula.
利用Dirichlet L-函数的均值定理以及Dedekind和的性质,研究了一个类似于Dedekind和的1/2次均值问题,并给出了一个较精确的渐近公式。
2.
A sum analogous to the dedekind sum and its 1/2 power mean value formula;
本文利用 Dirichet L-函数的均值定理以及 Dedekind和的性质研究了一个类似于Dedekind和的一次均值问题 ,并给出了一个较精确的渐近公式。
3.
A sum analogous to the Dedekind sum and its 1/3 power mean value formula;
利用 Dirichlet L-函数的均值定理以及 Dedekind和的性质研究了一个类似于 Dedekind和的 1 /3次均值问题 ,并给出了一个较精确的渐近公式。
补充资料：能量均分定理
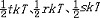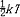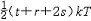| 能量均分定理 equipartition，theorem 在平衡态，物质分子能量分配的统计规律。在温度为T的平衡态，物质（气体、液体或固体）分子的每一个运动自由度都具有相同的平均动能  ，其中k是玻耳兹曼常量。用它可确定物质的内能和热容量。如果气体分子的平动、转动、振动自由度分别为t、r、s，则相应的平均动能分别为  ，因分子内原子的振动除动能外还有势能，且两者在一个周期内的平均值相等，故对于每一个振动自由度，还有 的平均势能。于是，分子的平均总能量为 ，对于理想气体，因分子间无相互作用，其内能就是上述分子平均能量与总分子数的乘积，只与温度有关，其热容量则与温度无关。气体分子能量按自由度的均分通过分子间的频繁碰撞得以建立和维持。外界供给气体的能量，通过器壁与气体分子以及气体分子之间的碰撞分配到各自由度上。对于液体和固体，能量按自由度均分是通过分子间很强的相互作用而实现的。 能量均分定理在经典物理范围内适用，要求能量可以连续地变化，它的困难也正源于此。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条