1) ring of Hurwitz series


Hurwitz幂级数环
2) ring of skew Hurwitz power series


斜Hurwitz幂级数环
3) the rings of Hurwitz series


Hurwitz级数环
1.
It is shown that if R is a domain and_ZR is torsion free,then the rings of Hurwitz series over R satisfies the ascending chain condition for principal ideals if and only if R satisfies the ascending chain condition for principal ideals.
证明了如果R是整环并且ZR无挠,则R上的Hurwitz级数环HR满足条件主理想升链条件(ACCP),当且仅当R满足条件ACCP。
4) ring of skew Hurwitz series


斜Hurwitz级数环
1.
On the ring of skew Hurwitz series;


斜Hurwitz级数环
6) skew power series ring


斜幂级数环
1.
Some extension of clean general rings is expounded based on it and it is shown that:(1) a general ring I is a clean general ring if and only if its power series ring is a clean general ring if and only if its skew power series ring is a clean general ring.
在此基础上讨论了一般clean环的几个扩张性质,得到如下结论:1)一般环I是一般clean环当且仅当I的形式幂级数环是一般clean环当且仅当I的斜幂级数环是一般clean环。
2.
It is shown that the skew power series ring R[[x; α]] is right p.


本文证明了斜幂级数环R[[x,α]]是右主拟Baer环当且仅当R是右主拟Baer环,并且R的任意可数幂等元集在I(R)中有广义交,其中I(R)是R的幂等元集。
3.
Given a c commutative ring R , obtains some conditions such that the skew power series ring R[[x,α]] and the trivial extension R∝M are also c commutative,and give examples to show these conditions are necessary.
对于 c-可换环 R,给出条件使得斜幂级数环 R[[x,α]]和 R的平凡扩张 R∝Μ也为 c-可换环 ,并用例子说明这些条件是必要的 。
补充资料:幂级数
| 幂级数 power series 一个无穷阶的多项式。又称为泰勒级数。它的一般形式是a0+a1(z-z0)+…+an(z-z0)n+…=  ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。 ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。有一种幂级数 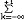 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有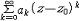 在圆|z-z0|<R上收敛,且 r<R,则级数 在圆|z-z0|<R上收敛,且 r<R,则级数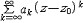 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形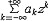 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条