1) nonparabolic energy band


非抛物型能带
2) nonparabolic band


非抛物性能带
4) nonparabolic
['nɔnpærə'bɔlik]


非抛物
1.
In the paper, we used some types of asymptotically nonnegative curvature to get some conditions of complete noncompact Riemannian manifold which is nonparabolic.
在本文中,主要讨论完备非紧的黎曼流形的Green函数的性质,主要利用各种渐进非负曲率和体积条件,得到在不同条件下流形是非抛物的结果。
5) non-parabolicity


非抛物线
1.
The band structure data being used in the simulations are based on the non-parabolicity method.
实验采用的是非抛物线模型计算电子的能带结构,模拟包含了声学声子散射,极性光学声子散射,压电散射,电离杂质散射,能谷间散射以及自散射等散射机理。
2.
The non-parabolicity multi-valley model is used to describe the conduction band structure of ZnS,in which two energy sub-bands are included.
模拟结果与全带Monte Carlo模拟得到的结果吻合得较好,但非抛物线多能谷模型比全带模型计算更简单。
6) nonparabolic end


非抛物端
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 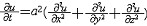 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式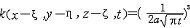 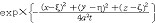 热传导方程初值问题的解可用基本解叠加而成,即 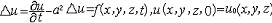 的解为 的解为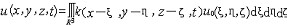 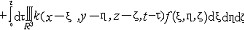 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 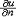 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条