1) base spline analysis


基数样条分析
2) cardinal Spline


基数样条
1.
The study on the construction of high cardinal Spline function;


关于高次基本基数样条函数构造的研究
3) cardinal B-spline


基数B-样条
1.
With the development of wavelet theory, the cardinal B-spline plays a more important role.
随着小波理论的发展,基数B-样条函数在数学与工程中发挥着越来越重要的作用。
4) Cardinal spline functions


基样条函数
6) cardinal B spline


基数B样条
补充资料:基数
| 基数 cardinal number 集合论中刻画任意集合所含元素数量多少的一个概念。又称势。两个能够建立元素间一一对应的集合称为互相对等集合。例如3个人的集合和3匹马的集合可以建立一 一对应,是两个对等的集合。根据对等这种关系对集合进行分类,凡是互相对等的集合就划入同一类。这样,每一个集合都被划入了某一类 。任意一个集合A所属的类就称为集合A的基数,记作 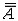 (或|A|,或cardA)。这样,当A 与B同属一个类时,A与B 就有相同的基数,即 (或|A|,或cardA)。这样,当A 与B同属一个类时,A与B 就有相同的基数,即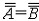 。而当 A与B不同属一个类时,它们的基数也不同。即 。而当 A与B不同属一个类时,它们的基数也不同。即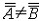 。 如果把单元素集的基数记作1,两个元素的集合的基数记作2,等等,则任一个有限集的基数就与通常意义下的自然数一致 。空集 。 如果把单元素集的基数记作1,两个元素的集合的基数记作2,等等,则任一个有限集的基数就与通常意义下的自然数一致 。空集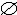 的基数也记作σ 。于是有限集的基数也就是传统概念下的“个数”。但是,对于无穷集,传统概念没有个数,而按基数概念,无穷集也有基数,例如,任一可数集与自然数集N有相同的基数 的基数也记作σ 。于是有限集的基数也就是传统概念下的“个数”。但是,对于无穷集,传统概念没有个数,而按基数概念,无穷集也有基数,例如,任一可数集与自然数集N有相同的基数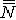 ,即所有可数集是等基数集。不但如此,还可以证明实数集R与可数集的基数不同,即 ,即所有可数集是等基数集。不但如此,还可以证明实数集R与可数集的基数不同,即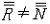 。所以集合的基数是个数概念的推广。基数可以比较大小。假设A,B的基数分别是a,β,即 。所以集合的基数是个数概念的推广。基数可以比较大小。假设A,B的基数分别是a,β,即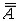 =a, =a,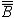 =β,如果A与B的某个子集对等,就称 A 的基数不大于B的基数,记作a≤β,或β≥a。如果 a≤ β,但a≠β( 即A与B不对等 ),就称A的基数小于B的基数,记作a<β,或β>a。基数可以进行运算 。设 =β,如果A与B的某个子集对等,就称 A 的基数不大于B的基数,记作a≤β,或β≥a。如果 a≤ β,但a≠β( 即A与B不对等 ),就称A的基数小于B的基数,记作a<β,或β>a。基数可以进行运算 。设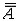 =a , =a ,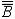 =β,且 A∩B= =β,且 A∩B=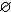 ,则规定 ,则规定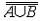 为a 与β之和记作 为a 与β之和记作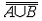 =a +β。设 =a +β。设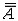 =a, =a,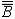 =β,A×B为 A与B的积集,规定 =β,A×B为 A与B的积集,规定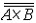 为 a 与β的积,记作 为 a 与β的积,记作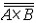 =a·β。 =a·β。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条