1) parabolic equation algorithm


抛物方程算法
2) parabolic equation method


抛物线方程算法
1.
The parabolic equation method,which is an efficient and fast numerical approach based on paraxial approximation of the wave equation,models energy propagation in a cone centered on the paraxial direction.
抛物线方程算法是建立在波动方程轴向近似基础上的一种数值方法,该方法假设电磁波能量沿抛物线轴向的锥形区域传播。
3) rotated parabolic equation method


旋转抛物线方程算法
1.
The rotated parabolic equation method was presented to compute the bistatic radar cross section(RCS).
并提出了旋转抛物线方程算法,实现了目标任意角度雷达散射截面的快速计算。
4) parabolic equation


抛物方程法
1.
Analysis of radio propagation in partly forested terrain environment using parabolic equation approach;
基于抛物方程法的部分森林覆盖山区电波传播分析
2.
Analysis of radio propagation over rough sea surface with parabolic equation


基于抛物方程法的粗糙海面电波传播分析
3.
Because atmospheric duct have a great effect on radio propagation,the technique of dealing with atmospheric duct is presented for inverse diffraction parabolic equation.
无源定位是近来的一个研究热门课题,逆绕射抛物方程法(IDPELS)能对发射源进行定位;但是传统IDPELS对复杂环境的处理能力有限,影响了其定位的精度。
5) parabolic equation method


抛物方程方法
1.
In this thesis the parabolic equation methods based on the higher-order Pade approximation are successfully applied to establish seismo-acoustic propagation model.
论文中应用基于Pade高阶近似的抛物方程计算格式建立了地声传播模型,实现了对声速、海深等环境变量随距离变化情况下的声场计算;重点分析了能量守恒和坐标旋转两种倾斜流体-弹性体边界条件处理方法;并在Matlab环境下编写了基于Pade高阶近似的抛物方程方法声场计算程序,通过与其它模型计算结果的比较分析检验了算法的计算精度。
2.
The parabolic equation method has been used widely in the electromagnetic wave propagation model and becomes the main tool to resolve the problem of electromagnetic wave propagation.
抛物方程方法已经被广泛地应用于电磁波传播模型,并成为解决电磁波传播问题主要的工具。
6) parabolic equation technique


抛物型方程方法
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 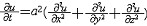 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式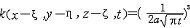 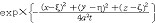 热传导方程初值问题的解可用基本解叠加而成,即 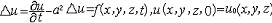 的解为 的解为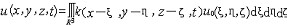 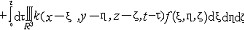 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 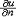 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条