1) parabolic equation


抛物方程
1.
Application of the wide-angle parabolic equation under impedance boundary condition;


宽角抛物方程在阻抗边界条件下的应用
2.
Blow-up of nonnegative radial solutions for a family of parabolic equations in bounded domain in RN;
R~N中有界域上的一类抛物方程非负径向解的爆破问题
3.
Renormalized solutions of a class of strongly degenerate quasilinear parabolic equations;


一类强退化拟线性抛物方程的重整化解
2) parabolic equations


抛物方程
1.
Constructive method for the Cauchy problem of parabolic equations and its mechanization;


抛物方程柯西问题的构造解法及机械化求解
2.
An alternating group method for four order parabolic equations;


四阶抛物方程的一类交替分组方法
3.
In this paper the oscillation property of a class of nonlinear parabolic equations with several delays is discussed.
研究了一类非线性时滞抛物方程在两类齐次边界条件下解的振动性质,获得了判别其所有解振动的充要条件,并通过实例对主要结果进行阐明。
3) parabolic equation


抛物线方程
1.
Comparisons of two different parabolic equation methods for electromagnetic computation;


两种抛物线方程算法在电磁计算中的比较
2.
Calculation of scatterers with edges with the improved parabolic equation;


基于改进的抛物线方程方法求解棱边散射体
3.
2-D electromagnetic scattering calculations with the parabolic equation;


基于抛物线方程求解二维电磁散射问题
5) parabolic equation systems


抛物方程组
1.
Partial regularity for weak solutions of a class of quadric increasing triangular parabolic equation systems;
一类二次增长的三角形抛物方程组弱解的部分正则性
2.
However,there are only a few results about regularity for weak solutions of nonlinear parabolic equation systems.
二次增长的非线性抛物方程弱解的正则性研究已有了比较完备的结果,但对于非线性抛物方程组弱解的正则性研究取得的成果还不多,有关文献证明了对角型抛物方程组的弱解在一定条件下是HO¨lder连续的。
6) parabolic partial differential equation


抛物型方程
1.
In this paper,the author studies the distribution of the solutions of the parabolic partial differential equations.
通过分部积分法、Cauchy不等式和Gronwall不等式来研究一类抛物型方程的解的分布情况,通过上述方法得出抛物型方程的能量模估计,最后由该能量模估计直接说明混合问题解的唯一性。
2.
A kind of finite volume element scheme for one dimensional parabolic partial differential equation with initial and Dirichlet boundary condition is presented,and it is proved that the scheme has second order convergence accuracy with respect to discrete L 2 norm and discrete H 1 seminorm.
针对一维抛物型方程初边值问题提出了一种新型的有限体积元格式 ,证明了该格式按离散 L2模及离散 H1半模具有二阶收敛精度 。
3.
An inverse problem for unknown source term in semilinear parabolic partial differential equation on bounded domain R n is considered in the following u t-Lu=φ(x,t)s(u)+γ(x,t), (x,t)∈Ω×(0,T), u(x,0)=u 0, x∈Ω, u n| Ω×(0,T) =g(x,t), u(x 0,t)=f(t), 0<t<T.
讨论了 Rn中有界域Ω上如下半线性抛物型方程未知源反问题ut- L u =φ(x,t) s(u) +γ(x,t) , (x,t)∈Ω× (0 ,T) ,u(x,0 ) =u0 , x∈Ω , u n| Ω× (0 ,T) =g(x,t) ,u(x0 ,t) =f (t) , 0
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 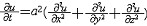 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式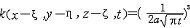 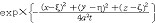 热传导方程初值问题的解可用基本解叠加而成,即 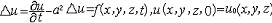 的解为 的解为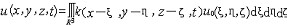 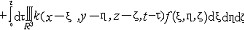 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 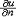 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条