1) Hamilton-Jacobi equation


哈密顿-雅可比方程
1.
Hamilton-Jacobi equation for one-dimensional continous system;


一维连续系统的哈密顿-雅可比方程
2) Hamilton Jacobi equation


哈密尔顿-雅可比方程
3) hamilton jacobi's equation


哈密顿雅可比方程
4) Hamilton_Jacobi_Bellman equation


哈密顿·雅可比·贝尔曼方程
1.
A Hamilton_Jacobi_Bellman equation with the Neumann boundary condition associated with this semigroup was obtained.
研究一类半空间上带泊松跳的反射扩散过程的随机最优控制问题· 得到关于这一控制问题的非线性Nisio半群 ,和联系这一半群的带Neumann边界条件的哈密顿·雅可比·贝尔曼方程· 讨论这一类方程的粘性解的存在唯一性等问题· 证明该控制问题中的价值函数是这一方程的一个粘性解
5) Hamilton-Jacobi-Bellman equation


哈密顿-雅可比-贝尔曼方程
6) Hamilton-Jacobi equation


哈密顿-雅克比方程
1.
In this paper we use knowledge from weak KAM theory and combine with analysis,topology and calculus of variations to Study the relation which is between the Peierls barrier,Ma(?) critical action and viscosity solutions of the time periodic Hamilton-Jacobi equation.
本文利用弱KAM理论,结合分析、拓扑及变分等数学工具,研究Peierls障碍函数和Ma(?)临界作用函数与时间周期的哈密顿-雅克比方程的粘性解之间的关系。
补充资料:哈密顿-雅可比方程
| 哈密顿-雅可比方程 Hamilton-Jacobi equation 分析力学中用以求解正则方程的一个偏微分方程 。由CGJ雅可比在W.R.哈密顿研究工作基础上给出而得名 。对于 N 个自由度的完整系统 ,此方程可写为 :  +H(q1,q2,…,qN; +H(q1,q2,…,qN;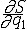 , ,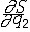 ,…, ,…,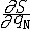 ;t)=0,式中H=T2-T0+V为哈密顿函数 ,其中V是用广义坐标qi (i=1,2,…,N)和时间t表示的势函数,T2和T0分别为动能T 中用广义动量表示的二次齐次式和零次齐次式(即不含pi,仅含qi和t之式);S为哈密顿主函数。若自方程求出包含N个任意常数( a1,a2,…,aN)的一个解(称全积分)S(q1,q2,…,qN;a1,a2,…,aN;t),则由 ;t)=0,式中H=T2-T0+V为哈密顿函数 ,其中V是用广义坐标qi (i=1,2,…,N)和时间t表示的势函数,T2和T0分别为动能T 中用广义动量表示的二次齐次式和零次齐次式(即不含pi,仅含qi和t之式);S为哈密顿主函数。若自方程求出包含N个任意常数( a1,a2,…,aN)的一个解(称全积分)S(q1,q2,…,qN;a1,a2,…,aN;t),则由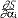 =-βi(β是常量), =-βi(β是常量),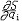 =pi(i=1,2,…,N)就能求出该系统正则方程的通解:pi=pi(t;a1,…,aN ;β1,…,βN),qi=qi(t;a1,…,aN;β1,…,βN)(i=1,2,…,N)。对许多力学实际问题,可以通过分离变 量法求出哈密顿-雅可比方程的全积分。对于工程上的保守系统,用此法计算繁琐,但它对天体力学的摄动法却大有帮助。 =pi(i=1,2,…,N)就能求出该系统正则方程的通解:pi=pi(t;a1,…,aN ;β1,…,βN),qi=qi(t;a1,…,aN;β1,…,βN)(i=1,2,…,N)。对许多力学实际问题,可以通过分离变 量法求出哈密顿-雅可比方程的全积分。对于工程上的保守系统,用此法计算繁琐,但它对天体力学的摄动法却大有帮助。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条