1) delay parabolic differential equation


时滞抛物方程
1.
Oscillation of delay parabolic differential equations;


具有时滞抛物方程的振动性
3) delay parabolic equation


时滞抛物型方程
1.
In general,the exactsolutions can be given only for few delay parabolic equations,In practice, people often usenumerical methods to obtain its approximate solution.
一般情况下,只有极少数时滞抛物型方程能够获得精确的解析表达式,在实际应用中,人们常常用数值方法获得其近似解。
4) System of delay parabolic equations


时滞抛物型方程组
5) delay parabolic partial differential equation


时滞抛物偏微分方程
1.
The present paper deals with oscillatory properties of solutions for a class of nonlinear impulsive neutral delay parabolic partial differential equations and some new sufficient criteria for oscillation of the equations are obtained under Robin and Dirichlet boundary value conditions via impulsive neutral differential inequalities of first order.
研究一类非线性脉冲中立型时滞抛物偏微分方程解的振动性,借助一阶脉冲中立型微分不等式,获得了该类方程在两类不同边值条件下振动的若干新的充分性判据。
6) neutral type delay parabolic differential equation


中立型时滞抛物型方程
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 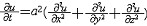 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式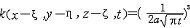 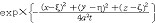 热传导方程初值问题的解可用基本解叠加而成,即 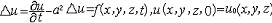 的解为 的解为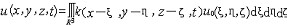 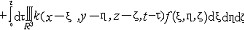 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 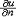 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条