1) trigonometric parametric curves


三角参数曲线
1.
A class of quasi-cubic trigonometric parametric curves based on {1,sin,cos,sin2 } is presented,which are called QCT-curves,including QCT-Ferguson curve,QCT-Bézier curve and uniform QCT-B spline curve.
给出了一组基于函数空间{1,sin,cos,sin2}的类三次三角参数曲线,称之为QCT-曲线,主要包括QCT-Ferguson曲线、QCT-Bézier曲线及均匀QCT-B样条曲线。
3) tri-parameter curve


三参数曲线
4) Cubic parametric curve


三次参数曲线
1.
So finally we get the cubic parametric curve with the minimum energy.


给定四个数据点,中间两点的参数分别取为0和1,然后对这四个点构造三次参数曲线,对于构造的曲线, 用曲线的能量建立目标函数,未知的两个参数作为目标函数的极小值点,求解能量的极小值点,从而得到两未知参数的值,最终得到能量最小的三次参数曲线。
5) cubic parametric curve segment


三次参数曲线段
1.
two parameters in respect to the extreme value points of cubic parametric curve segment r (t) are used to control the shape of r(t) .
本文利用三次参数曲线段r(t)极值,点的多数值t。
补充资料:UG编缉曲线参数
除非共享这是那些常常被忽略不被发现的直观拾取中之一。
当利用 Edit ->Curve-> Trim 你通常选择边界对象,跳过一选择步然后选择被修剪的曲线。你自然地一次选择一条曲线。
如图所示,为了直观地拾取被修剪的曲线,可以在图形窗口中拖拽一矩形与被修剪区相交。
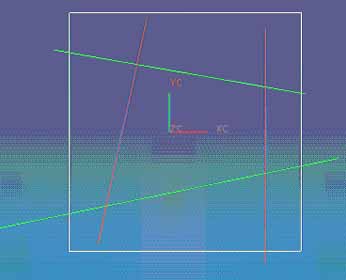 | 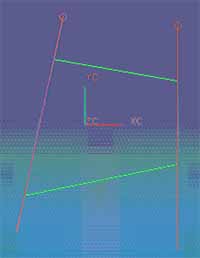 |
矩形窗口选择
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条