|
|
|
说明:双击或选中下面任意单词,将显示该词的音标、读音、翻译等;选中中文或多个词,将显示翻译。
|
|
|
1) reduction
[英][rɪ'dʌkʃn] [美][rɪ'dʌkʃən]

化归
1.
The Reduction of Aristotelian Modal Syllogism;

亚里士多德模态三段论的化归
2) induction
[英][ɪn'dʌkʃn] [美][ɪn'dʌkʃən]

化归
1.
It is introduced several kinds of inductions such as the transformations from generality to specialty,from number to shape,from reverse to obverse,from definite to indefinite,from motion to rest,from complexity to simplicity.
化归是解决数学问题中最一般的原则。
3) transformation
[英][,trænsfə'meɪʃn] [美]['trænsfɚ'meʃən]

化归
1.
The purpose of this paper is to present some ways of transformation based on decomposition of trigonometric reasoned formula of integral calculus, and furthermore, it can promote student s ability of integral calculation and use of recursion serial.
结合积分的计算,分析积分递推式的化归问题,三角有理式在积分中的拆分法的化归问题,有利于促进学生对于积分的计算以及递推序列的巧妙应用等数学能力的培养。
2.
Applying theory to specific cases to analyse ideogical method of transformation of several problems,briefly problems the principle and significance of transformation method in monadic calculus.
扼要论述了化归的原则及意义 ,从理论和实例分析讨论了一元微积分中若干典型问题化归的基本方法 。
4) classification
[英][,klæsɪfɪ'keɪʃn] [美]['klæsəfə'keʃən]

化归
1.
The structwre and Classification of Higher Mathematics;

简析高等数学的结构与化归
2.
But if you use the classification and transformation,the problems will become very easy.

在解决数学问题时,常遇到一些直接求解较难甚至不能解决的问题,利用化归与转化思想可以使问题变得易于解决。
5) transforming
[英][træns'fɔ:m] [美][træns'fɔrm]

化归
1.
The paper reflects positive and negative of transforming through discussing the theory of transforming(including definition,thinking,method and principle) and in the application of transforming in maths teaching.
通过对化归理论(包括化归的界定、化归思想、化归方法和化归原理)的探讨及其化归在数学实践教学中的应用,反思了化归的积极方面与消极方面。
2.
With the development of the theory of mathematics method and it s popular application in mathematics field, the discussion of transforming became more and more ordinary.
随着数学教学方法论的深入研究及其在数学研究与教学中日益广泛的应用,关于"化归"的议论很多。
6) domestication
[英][də,mesti'keiʃən] [美][də,mɛstə'keʃən]

归化
1.
On literal translation free translation and foreignization domestication;

直译与意译和异化与归化的分析
2.
Language s acceptability:——A yardstick to choose between domestication and foreignization;
归化和异化间“度”的把握——从《傲慢与偏见》的不同历史译本窥探文化翻译的归化与异化问题
3.
The Debate Concerning Domestication and Foreignization in China;

中国当代译坛归化异化论争
补充资料:化归法
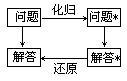
在解决问题的过程中,数学家往往不是直接解决原问题,而是对问题进行变形、转化,直至把它化归为某个(些)已经解决的问题,或容易解决的问题。 匈牙利著名数学家p·罗莎在她的名著《无穷的玩艺》一书中曾对“化归法”作过生动的比拟.她写道:“假设在你面前有煤气灶、水龙头、水壶和火柴,现在的任务是要烧水,你应当怎样去做?”.正确的回答是:“在水壶中放上水,点燃煤气,再把水壶放到煤气灶上.”接着罗莎又提出第二个问题:“假设所有的条件都不变,只是水壶中已有了足够的水,这时你应该怎样去做?”.对此,人们往往回答说:“点燃煤气,再把壶放到煤气灶上.”但罗莎认为这并不是最好的回答,因为“只有物理学家才这样做,而数学家则会倒去壶中的水,并且声称我已经把后一问题化归成先前的问题了.” 罗莎的比喻固然有点夸张,但却道出了化归的根本特征:在解决一个问题时人们的眼光并不落在问题的结论上,而是去寻觅、追溯一些熟知的结果,尽管向前走两步,也许能达到目的,但我们也情愿退一步回到原来的问题上去.利用化归法解决问题的过程可以简单地用以下框图表示:(右图) 把所要解决的问题,经过某种变化,使之归结为另一个问题*,再通过问题*的求解,把解得结果作用于原有问题,从而使原有问题得解,这种解决问题的方法,我们称之为化归法. 化归法是一种分析问题解决问题的基本思想方法.在数学中通常的作法是:将一个非基本的问题通过分解、变形、代换…,或平移、旅转、伸缩…等多种方式,将它化归为一个熟悉的基本的问题,从而求出解答.如学完一元一次方程、因式分解等知识后,学习一元二次方程我们就是通过因式分解等方法,将它化归为一元一次方程来解的.后来我们学到特殊的一元高次方程时,又是化归为一元一次和一元二次方程来解的.对一元不等式也有类似的作法.又如在平面几何中我们在学习了三角形的内角和、面积计算等有关定理后,对n边形的内角和、面积的计算,也是通过分解、拼合为若干个三角形来加以解决的.再如在解析几何中,当我们学完了最基本、最简单的圆锥曲线知识以后,对一般圆锥曲线的研究,我们也是通过坐标轴平移或旋转,化归为基本的圆锥曲线(在新坐标系中)来实现的.其它如几何问题化归为代数问题,立体几何问题化归为平面几何问题,任意角的三角函数问题化归为锐角三角函数问题来表示的例子就更多了.所以,掌握化归的思想方法对于数学学习有着重要的意义.总之,化归的原则是以已知的、简单的、具体的、特殊的、基本的知识为基础,将未知的化为已知的,复杂的化为简单的,抽象的化为具体的,一般的化为特殊的,非基本的化为基本的,从而得出正确的解答.
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条
|