1) mechanism approximating a straight line
近似直线机构
2) Approximate straight-line
近似直线
1.
The positions of connecting rod point that corresponding to the self-tangential curve,the curves with single tipped point and double tipped points and curve with approximate straight-line segments,which possess utmost values in track synthesis,had been made clear.
采用几何解析法研究曲柄摇杆机构特殊对称连杆曲线的产生条件,明确轨迹综合中极具价值的自切曲线、带单尖点和双尖点曲线,以及带近似直线段曲线所对应的连杆点位置,同时得到对称连杆曲线的形态种类及其分布规律。
3) Line Similarity Degree
直线近似度
4) straight-ray approximation
直射线近似
5) beeline approximation method
直线近似法
1.
Aiming at the normal maximum power point tracker (MPPT) algorithm’s some deficiencies in low tracing rate and concussion near the maximum power point, a new MPPT methods—beeline approximation method combined with perturbation and observation method with changing perturbation step was presented.
针对普通的最大功率算法在最大功率点振荡、追踪速度不高等缺点,提出了一种新的最大功率点跟踪控制方法——直线近似法结合变步长扰动观察法的最大功率追踪方法。
6) approximate straight-line locus
近似直线轨迹
补充资料：机械原理:直线运动机构
直线运动机构
使构件上某点作準确或近似直线运动的机构﹐大多由製造简便的转动副和杆状构件组成。由於加工高精度移动副已无困难﹐这种机构仅在仪錶和某些机械上尚有应用。这种机构分为近似直线运动和正确直线运动的两类。
瓦特﹐J.近似直线运动机构﹕19世纪初﹐为了代替当时笨重的齿扇链条机构﹐瓦特﹐J.利用并行运动原理製成一种近似直线运动机构(图 1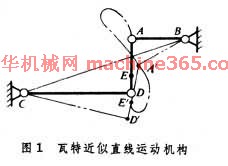
瓦特近似直线运动机构 )。这种机构处於中间位置时﹐AD ⊥AB ﹐AB CD ﹐AE ﹕DE =CD ﹕AB ﹐E 点轨跡有一段近似直线﹐其长度至少等於AD 。
波舍利準确直线运动机构﹕1864年波舍利发明準确直线运动机构﹐它是一个8杆机构。在图2a 波舍利準确直线运动机构 中﹐直线O 绕O 点转动﹐动点P 和Q 在沿直线O 移动的同时分别画出和两条曲线﹐若OP ×OQ =常数﹐则称为的互反曲线。若为以C 为圆心﹐以CO 为半径的圆弧(图2b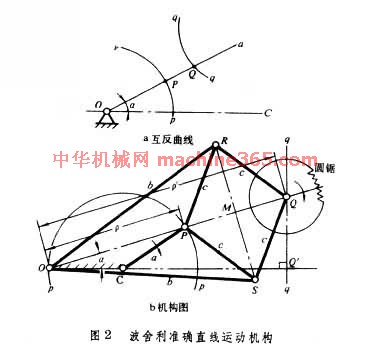
波舍利準确直线运动机构 )﹐则其互反曲线即为垂直於O 的直线。波舍利準确直线运动机构就是按照上述条件设计而成的。例如在锯床上﹐这种机构的Q 轴装上电动机和圆锯﹐摆动CP 杆﹐圆锯就能沿作直线切割。
此外﹐著名的直线运动机构尚有分别以契贝谢夫﹑罗伯茨命名的直线运动机构和以哈特﹑肯普﹑斯科特－拉塞尔命名的準确直线运动机构等。
使构件上某点作準确或近似直线运动的机构﹐大多由製造简便的转动副和杆状构件组成。由於加工高精度移动副已无困难﹐这种机构仅在仪錶和某些机械上尚有应用。这种机构分为近似直线运动和正确直线运动的两类。
瓦特﹐J.近似直线运动机构﹕19世纪初﹐为了代替当时笨重的齿扇链条机构﹐瓦特﹐J.利用并行运动原理製成一种近似直线运动机构(图 1
瓦特近似直线运动机构 )。这种机构处於中间位置时﹐AD ⊥AB ﹐AB CD ﹐AE ﹕DE =CD ﹕AB ﹐E 点轨跡有一段近似直线﹐其长度至少等於AD 。 波舍利準确直线运动机构﹕1864年波舍利发明準确直线运动机构﹐它是一个8杆机构。在图2a 波舍利準确直线运动机构 中﹐直线O 绕O 点转动﹐动点P 和Q 在沿直线O 移动的同时分别画出和两条曲线﹐若OP ×OQ =常数﹐则称为的互反曲线。若为以C 为圆心﹐以CO 为半径的圆弧(图2b
波舍利準确直线运动机构 )﹐则其互反曲线即为垂直於O 的直线。波舍利準确直线运动机构就是按照上述条件设计而成的。例如在锯床上﹐这种机构的Q 轴装上电动机和圆锯﹐摆动CP 杆﹐圆锯就能沿作直线切割。 此外﹐著名的直线运动机构尚有分别以契贝谢夫﹑罗伯茨命名的直线运动机构和以哈特﹑肯普﹑斯科特－拉塞尔命名的準确直线运动机构等。
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条