1) random metric space
随机度量空间
1.
The general ordering principle in nonlinear functional analysis is generalized to random metric spaces and a random ordering principle is given in this paper, the random generalizations of Ekeland s variation principle and Caristi s fixed - point theorem are proved, many previous results are unified and generalized, and some new fixed - point theorems are obtained.
将非线性泛函分析中的一般定序原理推广到随机度量空间,得到了一个随机的定序原理;证明了Ekeland变分原理和Caristi不动点定理的随机推广;统一和推广了文献中的许多结果;得到了一些新的不动点定理。
2.
Three contraction properties (probabilistic contraction, random contraction, metric contraction),random Ekeland variational principleand randomCaristi fixed pointtheorem,and the relationships between them and completeness are discussed in random metric space.
研究了随机度量空间的三种压缩(概率压缩、随机压缩、度量压缩)的性质、随机Ekeland变分原理和Caristi不动点定理以及它们与完备性之间的相互关系。
2) random quasi-metric family space
随机准度量族空间
1.
in this paper, we introduce the concepts of quasi-metric family spaces with an index set, and discuss the relationship between quasi-metric family spaces with an index set, probabilistic quasi-metric family spaces and random quasi-metric family spaces.
引入了带指标的准度量族空间的概念，讨论了带指标的准度族空间与概率准度量族空间和随机准度量族空间之间的关系，建立了这些空间的一些性质，研究了这些空间的等矩同构。
3) Randomized Logic Metric Space
随机逻辑度量空间
1.
The concept of randomized logic metric space is also introduced and it is proved that the new built randomized concepts are extensions of the corresponding concepts in quantified logic.
利用赋值集的随机化方法,在三值R_0命题逻辑系统中提出了公式的随机真度和随机距离,建立了随机逻辑度量空间。
4) Stochastic Quantum Space(SQS)
随机量子空间(SQS)
5) stochastic stiffness
空间随机刚度
1.
Exact solution of the bending of circular plate with spatially stochastic stiffness;
具空间随机刚度薄圆板的轴对称弯曲精确解
6) random space
随机空间
1.
Method for structural reliability analysis in generalized random space;
广义随机空间内的一次可靠度分析方法
补充资料：度量空间
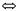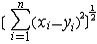| 度量空间 metric space 具有度量的抽象空间，设X是一个集合，若有定义在X×X上的非负实值函数d，满足①d（x，y）≥0，d（x，y）＝0  x＝y； ②d（x，y）＝d（y，x）；③d（x，z）≤d（x，y）＋d（y，z），则称（X，d）是度量空间，d称为距离或度量。这是最接近于欧几里得空间的抽象空间。利用度量可很自然地将欧几里得空间上点的邻域、开集、闭集，收敛序列以及连续映射等概念推广到一般度量空间，也能将一致连续的概念推广到度量空间。由于19世纪末集合论产生后，实变函数及泛函分析的发展，需要规定函数间的距离，因而抽象出度量、度量空间的概念，其创始人是M.R.弗雷歇。常见的度量空间有：n维欧几里得空间（Rn,d）：Rn＝｛（x1，…，xn）｜xi∈R，i＝1，2，…，n ｝，d（x，y）＝  ，其中x＝（x1，x2，…， xn），y＝（y1，y2，…，yn）。希尔 伯特空 间（l2；d）：l2＝｛（x1，x2，…，xn…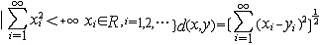）  ， 其中x ＝( x1，x2 ，…），y＝（y1，y2，…）∈l2。函数空间(ρ[0，1］，d)：C[0，1］＝｛f：f为[0，1］上的实值连续函数｝，对任意f，g∈C[0，1］，d(f，g)＝max｛｜f（x）－g（x）｜｝。 x∈[0，1］ 对度量空间（X，d）可引进拓扑结构，即以包含开球B（x，r）＝｛y∈X｜d（ x，y）＜r ｝的集为邻域定义拓扑，称为d所诱导的拓扑。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条