1) function space


函数空间
1.
The compactness of a new function space;


一个新的函数空间的紧致性
2.
A note on the algebraicity of domain function spaces


Domain函数空间代数性的一个注记
3.
By the new method, which utilizes function approaches theory, projection operator theory and multi-resolution analysis, the telegraphic equation can be projected into a function space, which is spanned by the orthogonal basis function relates to variable t in an given binary resolution, and then an vector equation with only one variable of distance x is presented.
利用函数逼近、投影变换和多分辨分析理论将输电线路电报方程组投影到由一个关于时间变量t的基函数,在某个二进分辨率下通过位移张成的函数空间中,得到一个只关于距离变量x的向量微分方程组。
2) function spaces


函数空间
1.
A generalization of the invariantly cometrizable property is given for the set-open topology for function spaces.
本文对函数空间在集开拓扑下的不变余度量性质进行了推广,给出了函数空间在紧开拓扑和点收敛拓扑下不变余度量化的充要条件。
2.
In this paper, the theoretical properties of some function spaces in the unit disk are studied.
本文主要研究了单位圆盘上一些函数空间的分析性质,主要是以下两个方面,这些结果均推广了已知的结论。
3) functional space


函数空间
1.
The dynamics, stability and control problem of a kind of infinite dimensional system are studied in the functional space with the method of modern mathematics.
利用现代数学方法 ,在函数空间中研究了一类无穷维系统动力学、稳定性与控制问题· 首先提出并建立了具有阻尼、陀螺部件和约束阻尼的多拓扑结构多挠体分布参数系统动力学控制模型 ;其次给出并论证了多体挠性结构特征、系统分析结果———可控可观性充要条件、稳定性理论和系统的渐近性质· 研究的结果扩充和发展了本领域关于多挠体系统动力学与控制的理论成果 ,具有重要的工程意义
4) wave function space


波函数空间
5) full function space


全函数空间
1.
The result is proven in the paper that lat B is a (C-Ⅱ) and equal-module full function space, then P_BB_S has the Radon-Riesz property if and only if all B_S (s∈S) have the Radon-Riesz property, and it generalizes the corresponding result~([4]).
证明了若有有限逼近的全函数空间B有(C-Ⅱ)性质和等模性质,则置换空间PBBS有Radon-Riesz性质当且仅当每个BS有Radon-Riesz性质,其结果推广了文[4]中Radon-Riesz性质在置换空间上的提升结果。
6) space weight function


空间权函数
补充资料:函数空间
| 函数空间 functional space 由定义在一般集合上的函数组成的集合,并且在 集合中装备了一定的几何结构。例如取X={f∶f为定义在[a,b]上的连续函数}, 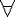 f∈X,定义‖f‖= f∈X,定义‖f‖=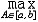 |f(t)|,称之为f的范数,范数是通常长度概念的拓广 ,利用范数可定义X中任何两个元素(或点)之间的距离ρ(f,g)=‖f-g‖,则X就是一个函数空间,在X中可以谈论点列(即函数列)的收敛问题:{fn} |f(t)|,称之为f的范数,范数是通常长度概念的拓广 ,利用范数可定义X中任何两个元素(或点)之间的距离ρ(f,g)=‖f-g‖,则X就是一个函数空间,在X中可以谈论点列(即函数列)的收敛问题:{fn}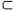 X,f∈X,fn→f,当且仅当ρ(fn,f)=‖fn-f‖= X,f∈X,fn→f,当且仅当ρ(fn,f)=‖fn-f‖=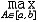 |fn (t)-f(t)|→0 。此外,还可在X中规定加法和数乘运算如下 : |fn (t)-f(t)|→0 。此外,还可在X中规定加法和数乘运算如下 : f ,g∈X, α∈IR,则定义(f+g)(t)=f(t)+g(t),(αf)(t)=α·f(t),则 X是一个线性空间,事实上X为一完备的线性赋范空间,即巴拿赫空间。常用的函数空间不一定有以上空间那样好的性质,但一般来说为线性拓扑空间,空间中的元素不仅满足线性关系,并且线性运算关于拓扑是连续的,有可能研究连续、有界、可微等分析性质。 f ,g∈X, α∈IR,则定义(f+g)(t)=f(t)+g(t),(αf)(t)=α·f(t),则 X是一个线性空间,事实上X为一完备的线性赋范空间,即巴拿赫空间。常用的函数空间不一定有以上空间那样好的性质,但一般来说为线性拓扑空间,空间中的元素不仅满足线性关系,并且线性运算关于拓扑是连续的,有可能研究连续、有界、可微等分析性质。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条