1) total differential
全微分
1.
It had also been discovered that the differential of the potential function of fold catastrophe model was the total differential.
定量阐述了在岩体系统准静态形变路径不同的位置处,系统有不同的总势能;岩体系统动力失稳释放的能量?Π与失稳起始点j、终止点s之间的能量关系为Πs=Πj+△Π,其中△Π<0;发现折迭突变模型势函数的微分是全微分,利用全微分的积分值与路径无关的性质,对在普通试验机上加载发生脆性破坏的岩样,在伺服试验机上通过油缸排油对外界输出能量,使岩样以渐进形式破裂的现象进行阐述。
2.
There are many affecting aspects of ejecting coefficient of water ejector, including area ratio, working pressure, ejecting pressure and outlet pressure with the method of variable total differential, the expres-sions of ejecting coefficient are obtained in this paper.
影响水喷射器引射系数的因素很多,包括面积比、工作压力、引射压力及出口压力等,本文运用变量全微分的方法推出了这些影响因素改变时对于引射系数影响的具体表达式,井通过计算数据,分析了这些因素的影响次序。
3.
It is pointed out that the term “heat δQ and work δW are not total differential.
从数学和物理两个方面说明“微热与微功不是全微分”这一结论的确切意
2) complete differential
全微分
1.
Tolerance of the system was synthesized, applying complete differential and genetic algorithm by assuming the production cost as goal function, then the tolerance of every part was calculated.
建立了构件尺寸公差与制造成本之间的数学模型,并以制造成本最小为优化目标函数,采用全微分法和遗传算法,分析计算了连杆机构中杆长尺寸公差和铰链间隙的公差分配,进而推算出了其他各构件几何尺寸的公差。
2.
Tracing algorithm for Thevenin equivalent parameters based on complete differential equation was presented in consideration of parameter variation during calculation.
考虑戴维南等值参数在跟踪计算过程中不断变化的实际情况,提出基于全微分的戴维南等值参数跟踪计算方法。
3) total differentiation
全微分
1.
In this paper,using total differentiation method and variation of constants,we give general solution formula of Bernoulli equation with different methods.
本文使用全微分法和常数变易法,从不同角度给出伯努利方程通解的公式。
4) perfect differential
全微分
1.
On the invariability in perfect differentials in the derivation of variable function;
全微分形式不变性在多元函数求导中的作用
2.
Introducing some common methods for the derivation of implicit function determined by system of equations: to explicitize implicit function,to differentiate equation,to use perfect differential.
介绍求解由方程组确定的隐函数求导问题常用的几种方法:将隐函数显化,方程两边直接求导,利用全微分。
5) total differential method
全微分法
1.
Having common difference matrixing of angle by total differential method;
用全微分法进行角度公差换算
6) Total derivative term
全微分项
补充资料：全微分
| 全微分 complete differential 如果二元函数z＝f(x，y)在P(x，y)点的增量Δz＝f(x＋Δx，y＋Δy)－f(x，y) 能表示为Δz＝AΔx＋BΔy＋0(ρ)，其中 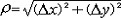 ，A、B，是与Δx和Δy无关的常数，0（ρ）表示当ρ→0时比ρ高阶的无穷小量， 即0(ρ)趋于0的速度比ρ趋于0的速度要快，AΔx＋BΔy成为函数增量的主要部分，并且关于Δx、Δy是线性的，则说二元函数z＝f（x，y)Ｔ赑点可微，称AΔx＋BΔy为函数的全微分。记为dz＝AΔx＋BΔy，因自变量的微分等于改变量，所以dz＝Adx＋Bdy。与一元函数所不同之处是，在一元函数中，函数在P点可微与可导是等价的，但对二元函数来说，由可微可推出两个偏导数(见偏导数)存在，但光从两个偏导数存在还不能得出可微的结论。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条