2) holomorphic differential form
全纯微分形式
3) differential form
微分形式
1.
The above conclusion is demonstrated in the light of poincare theorem, it is demonstrated by using contraction (interior product) of vector field and differential form as well as operation of exterior differentiation.
运用向量场与微分形式的缩并 (内积 )和外微分运算 ,并依照 Poincare定理论证电荷的运动规律可确定电磁场的运动规
2.
By estimating the koppelman kernel on Complex Manifolds, the difference between the koppelman kernel on complex manifolds and the Bochner Martinelli koppelman on C n was obtained;and then by utilizing the koppelman formula and the result as above, the jump formula of differential forms under Berndtsson transform on Complex manifolds was derived.
引入复流形上的Ｋｏｐｐｅｌｍ ａｎ 核与微分形式的Ｂｅｒｎｄｔｓｓｏｎ 变换， 并对复流上的Ｋｏｐｐｅｌｍ ａｎ 核进行估算，得出其与Ｃｎ 空间的Ｂｏｃｈｎｅｒ－Ｍａｒｔｉｎｅｌｌｉ－Ｋｏｐｐｅｌｍ ａｎ 核之差为Ｏ（－ ２ｎ ＋１ｎ ）。
3.
By the natural and harmonious relationship between differential forms and differential equations and between differential forms and vector analysis, we discuss the properties, which are covariant under the transformation of coordinates in the framework of differential forms, of particle motion in a central force field.
通过微分形式与微分方程和向量分析之间存在的自然而协调的关系，在微分形式框架下讨论了质点在有心力场中运动的特性并得出在坐标变换下其均是协变的
4) differential forms
微分形式
1.
The Hypo-elliptic Differential Forms on Smooth Manifolds;
光滑流形上微分形式的亚椭圆性
2.
Let X be a smooth oriented Riemannian n-manifold without boundary,l-form W be WT2 class of differential forms on X.
令X是一个光滑可定向的n维无边黎曼流形,l-形式W是X上的WT2类微分形式,如果它的结构常数v1、v2满足一定的条件,则对于dφ=ω的l-1-1形式φ的模满足Holder连续性。
5) ordinary differential form
常微分形式
6) exterior differential form
外微分形式
1.
The exterior differential form was pointed out to be the mathematical model of a lot of proposition in field theory.
建立了外微分理论与场论之间的一些对应法则,指出外微分形式是场论中众多命题的数学模型,得到用外微分运算解决场论中梯度、旋度、散度以及环量与通量的计算和几种重要的矢量场:梯度场、旋度场、调和场证明的新方法。
2.
Thenecessity and urgency were discussed that exterior differential form and some content of mordenmathematics were introduced in teaching.
对当前高等数学课教学内容严重滞后的现状作了系统分析，论述了在教学中引入外微分形式及当代数学部分内容的必要性和紧迫性。
3.
This paper introduces the concept of Finslerian exterior differential form and two exterior differential operators dh,dv,which are different from the general theory of Cartan s.
本文提出了一种与加当外微分法不同，但适用于芬斯拉几何的外微分理论，包括芬斯拉外微分形式与两个外微分算子ｄｈ，ｄｖ。
补充资料：全微分
| 全微分 complete differential 如果二元函数z＝f(x，y)在P(x，y)点的增量Δz＝f(x＋Δx，y＋Δy)－f(x，y) 能表示为Δz＝AΔx＋BΔy＋0(ρ)，其中 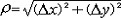 ，A、B，是与Δx和Δy无关的常数，0（ρ）表示当ρ→0时比ρ高阶的无穷小量， 即0(ρ)趋于0的速度比ρ趋于0的速度要快，AΔx＋BΔy成为函数增量的主要部分，并且关于Δx、Δy是线性的，则说二元函数z＝f（x，y)Ｔ赑点可微，称AΔx＋BΔy为函数的全微分。记为dz＝AΔx＋BΔy，因自变量的微分等于改变量，所以dz＝Adx＋Bdy。与一元函数所不同之处是，在一元函数中，函数在P点可微与可导是等价的，但对二元函数来说，由可微可推出两个偏导数(见偏导数)存在，但光从两个偏导数存在还不能得出可微的结论。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条