1) coupled parabolic equation dispersion problem


耦合型抛物方程弥散项
2) coupled parabolic system


耦合抛物方程组
1.
The homogenization of a coupled parabolic system is discussed carefully and the homogenization results are obtained.
详细讨论了多孔介质中一类耦合抛物方程组的均匀化过程,并给出了均匀化结果。
2.
This paper deals with coupled parabolic system ui=vp u,v,in (0,T) with nonlinear boundary conditions , where is a bounded domain with smooth boundary, p,q>0 and a,B>0 are constants.
考虑带非线性边界条件αu/αn=u~α,αu/αn=v~β,(x,t)∈αΩ×(0,T)的耦合抛物方程组u_t=v~p△u,v_t=u~q△v,(x,t)∈Ω×(0,T),其中ΩR~N为一具有光滑边界的有界区域,p,q>0和α,β≥0为常数。
3) coupled parabolic partial differential equations


抛物型耦合偏微分方程组
1.
Mixed finite element method for a class of coupled parabolic partial differential equations is presented.
针对一类抛物型耦合偏微分方程组给出了混合有限元方法 ,在引入椭圆投影的基础上 ,得到了与双调和方程同样的误差估计 。
4) elliptic parablic coupled system


椭圆抛物耦合方程组
5) Hyperbolic-parabolic coupled systems


双曲抛物耦合方程组
6) CNM------PEM


耦合简正波—抛物方程
补充资料:抛物型偏微分方程
| 抛物型偏微分方程 parabolic type,partial differential equation of 偏微分方程的一类。最典型的是热传导方程 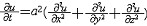 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式 (a>0) (1)基本解是点热源的影响函数。若在t=0时在(ξ,η,ζ)处给定单位点热源,即u0(x0,y0,z0,0)=δ(ξ,η,ζ)(δ为狄拉克函数),则当t>0时便引起在R3的温度分布,这就是基本解。用傅里叶变换可得到它的表达式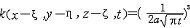 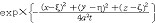 热传导方程初值问题的解可用基本解叠加而成,即 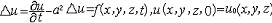 的解为 的解为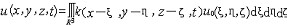 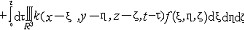 极值原理:一个内部有热源的传导过程,它的最低温度一定在边界上或初始时刻达到。更强的结论是 :如果t=T时在Ω内某一点达到最低温度 ,则在这个时刻以前(t<T时)u≡常数 ;又:若最低温度在t=T时边界¶Ω上某点P达到,则在这点上 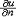 |P,Τ<0(n为外法线方向)。 |P,Τ<0(n为外法线方向)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条