1) tangential strain


切向应变
1.
The approximate formula of the changing value of wall thickness of the inner and outer side of the tube and the formula of the tangential strain are presented,which may be applied to practical production after amending.
通过大量管材弯曲试验,分析了沿弯曲线的切向和管壁厚方向的应力应变状态,给出弯管内、外侧管壁厚变化量和切向应变的近似计算公式。
2.
It was found that during the no_mandrel bending forming process of minor diameter tube,the actual tangential strain along pipeline direction was approximately distributed in parabola,and the maximum strain appeared around the intermediate section of the bending angle.
作为管材弯曲变形机理实验研究的一部分,通过大量实验结果证明了小直径管无芯弯曲成形过程中,沿管线方向的真实切向应变近似呈抛物线形分布,最大应变产生在弯曲角中部附近。
2) transverse shearing strain


横向剪切应变
1.
The nonlinear equation includes two nonlinear terms caused by finite deformation and double geometric dispersion effects caused by transverse inertia and transverse shearing strain.
在同时引入横向惯性和横向剪切应变的情况下,导出了有限变形弹性圆杆的非线性纵向波动方程,方程中包含了二次和三次的非线性项以及由横向剪切与横向惯性导致的两种几何弥散效应。
3) tangential stress


切向应力
1.
Based on the Inglis formula, which calculates the tangential stress of the surrounding rock of geological stress field in different circumstances, programme is developed to compute the corresponding tangential stress of the surrounding rock of several underground plants, for instance, Ertan project of Sichuan according to different directions of longitudinal axle.
从地下洞室周边切向应力的英格里(Inglis)公式出发,提出针对不同环境的地应力场进行地下厂房纵轴线方位优选的简便方法,并编程计算了四川二滩等多个地下厂房不同纵轴线方向所对应的洞室周边切向应力,分析不同纵轴线方向条件下洞室周边切向应力的极值,并与实际工程所选取的纵轴线方向所对应的切向应力值比较,讨论了工程所选纵轴线的合理性以及洞室周边应力的集中程度。
2.
The compulation formulas on radial stress,tangential stress and deflection were derived.


运用平板理论 ,分析了周边固定受同心环形线载荷作用环形圆板的应力 ,并且导出径向应力、切向应力及挠度的计算公式 ,为结构设计提供了方
3.
The calculation formulae of normal stress difference,tangential stress and moment acted on the inner cylinder for the flow of power-law fluid in annulus with the inner cylinder executing a planetary motion under motive bipolar coordinate system were given.
给出了运动双极坐标系下幂律流体在内管做行星运动的环空中流动时流体作用在内管外壁上的法向应力差、切向应力和扭矩的计算公式;以可视为幂律流体的CMC水溶液为例,利用幂律流体在内管做行星运动的环空中流动的流函数分布的数值解对该流动时流体作用在内管壁的法向应力差、切向应力和扭矩进行了数值计算,并分析了内管自转和公转速度、环空偏心度以及压力梯度对其的影响;还以水为例,把利用数值解绘制的法向应力差、切向应力和扭矩的分布曲线与解析解绘制的法向应力差、切向应力和转矩的分布曲线进行了对比,两者吻合较好,说明给出的幂律流体在内管做行星运动的环空中流动时流体作用在内管外壁上的法向应力差、切向应力和扭矩的计算公式以及数值计算方法是正确的。
4) tangent stress


切向应力
1.
The experiment analysis of gas seepage law in a single fracture under 3D stress is studied, theinfluence of tangent stress on the seepage law is focused, and the following conclusion has been made: the tangentdeformation has the same effect as normal deformation on fracture seepage law, In the end, an experientialformula of gas seepage law in a single fracture are brought forward.
研究了三维应力作用下,侧向应力对气体裂缝渗流规律的影响,得出裂缝剪切变形同裂缝法向变形一样,对气体裂缝渗流规律有显著的影响,并给出了同时考虑法向应力、切向应力和孔隙压影响的气体单一裂缝渗透系数的经验公式。
5) angular correction


切向变位
1.
It is presented that in gear-hobbing machine by unsnapping the change-gears and rotating the gear d,angular correction cutting will be simple and convenient and with high accuracy.
在新型输出机构———零齿差机构中 ,齿轮必须进行切向变位才能避免齿形干涉 。
6) tangentiai deformation


切向变形
补充资料:切应变
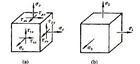
切应变
物体受力产生变形时,体内各点处变形程度一般并不相同。用以描述一点处变形的程度的力学量是该点的应变。为此可在该点处到一单元体,比较变形前后单元体大小和形状的变化。
在直角坐标中所取单元体为正六面体时,单元体的两条相互垂直的棱边,在变形后的直角改变量,定义为角应变或切应变,用γ表示。一点在x-y方向、y-z方向z-x方向的切应变,分加别为γxy、γyz、γzx。切应变以直角减少为正,反之为负。
说明:补充资料仅用于学习参考,请勿用于其它任何用途。