1) allais's paradox of system stimulation


制度激励悖论
2) encouragement paradox


激励悖论
3) institutional dilemmas


制度悖论
1.
This paper states that buffer organization is an effective organization for deregulation in higher education system, base on which I hold some new idea of institutional dilemmas in this paper.
本文认为,中介组织是我国高教系统进行分权的有效载体,在此基础上,利用经济学的相关知识,对我国高教系统分权中的"制度悖论"进行了新的解读。
4) incentive system


激励制度
1.
Reconstruction of Incentive Systems and Game Analysis of Pollution Control for Local Government;
地方政府治污的博弈分析与激励制度重构
2.
Comparative study of traits of human capital of professional athletes and incentive system;
职业运动员人力资本特性及其激励制度比较研究
3.
This article has discussed the environmental protection incentive system FOAK principle in China,constructed the innovative system of improving the incentive system of e.
当环境保护与经济发展遇到不可协调的矛盾时,如何有效实施环境保护制度创新,从而实现"保护环境是经济上必需的",是环境保护激励制度创新中的重要问题。
5) motivation system


激励制度
1.
Through expounding the stock option motivation system and its theoretical base, this paper analyzes the necessity of Multinational Corporations’ implementing the stock option motivation system and some problems that should pay attention to.
通过对股票期权激励制度及其理论基础的阐述,分析了跨国公司实施股票期权激励制度的必要性以及需要注意的问题。
2.
Through models, this paper analyses on the relations between enterprise motivation measures and individual efforts,and discusses on the principles of establishing motivation system and some problems relative to the evaluation of performances and achievements.
文章通过模型,分析了各种激励措施与个体努力程度的关系,讨论了企业激励制度建设的原则以及有关绩效评价问题。
3.
Effective technological innovation s motivation system plays an important role in pushing the enterprise forward and giving impetus to the economics.
市场经济和国家发展需要技术创新,而技术创新的积极活跃却有赖于激励制度。
6) encouraging system


激励制度
1.
The arti cle points out the modes and principles on the encouraging system of library.


指出图书馆激励制度的模式、原则及激励制度的设
补充资料:悖论
| 悖论 paradox 自相矛盾的说法。即如果承认这个说法正确,就能推出这个说法不正确,反之,如果承认这个说法不正确,却又能推出这个说法正确。1900年前后在集合论中出现了一些悖论,例如罗素悖论和康托尔悖论。 ①罗素悖论。把所有满足条件x不属于x的集合x组成一个集合A,即 A是一切不属于自身的集合所组成的集合, A={x|x 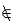 x}。在初期的集合论中,这样定义一个集合是允许的,既然承认A是一个集合,那么它是否满足A x}。在初期的集合论中,这样定义一个集合是允许的,既然承认A是一个集合,那么它是否满足A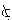 A?假定A A?假定A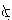 A,那么A属于所定义的集合,即A∈A,矛盾;假定A∈A,于是A不属于这样定义的集合,即A A,那么A属于所定义的集合,即A∈A,矛盾;假定A∈A,于是A不属于这样定义的集合,即A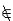 A,也自相矛盾。 A,也自相矛盾。②康托尔悖论。设V 是由一切集合所组成的集合。考虑集合V的基数 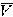 ,康托尔证明,V的幂集P(V)的基数 ,康托尔证明,V的幂集P(V)的基数 (V)大于 (V)大于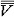 ;但根据V的定义,任何集合都是V的子集,因而不存在其基数大于 ;但根据V的定义,任何集合都是V的子集,因而不存在其基数大于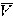 的集合,自相矛盾。 的集合,自相矛盾。这些悖论在当时震动了数学界。产生悖论的原因是那时的集合论本身还不够严格。为了避免悖论,数学家们重新研究集合的概念,进行严格整理,于是产生了多种集合论公理系统。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条