1) hyperbolic sine constitutive equation


双曲线本构方程
2) hyperbolic curve equation


双曲线方程
1.
Hyperbolic curve equation(X_t = b-a/t) was used to fit the accumulated nutrient dissolving percentage and the slow-release index(SRI) calculated from b and a values of the equation was used to evaluate the nut.
在实验室条件下,采用简化的工艺制备了对氮、磷、钾三元素均有部分缓释作用的复混肥(化学缓释肥),用特定淋洗装置测定肥料各养分随时间的溶出率,通过双曲线方程Xt=b-a/t对其养分累计溶出率与时间的关系进行拟合,以方程常数b和a计算出的缓释指数(SR I)来定量评价肥料缓释特性,同时进行盆栽试验,探讨了缓释指数与复混肥中相应缓释添加剂百分含量(X)之间、各复混肥处理的油菜产量与复混肥中缓释添加剂总含量(X')之间的关系。
4) hyperbolic constitutive model


双曲线本构模型
1.
Parameter back-analysis of hyperbolic constitutive model in soils;


土体双曲线本构模型的参数反演
5) rectangular hyperbola method


等轴双曲线方程
6) nonlinear hyperbolic equation


非线性双曲方程
1.
On a class of nonlinear hyperbolic equations in unbounded domain;


无界域上的一类非线性双曲方程的局部可解性
2.
Energy decay of global solution of initial boundary value problem for a class of nonlinear hyperbolic equation;
一类非线性双曲方程初边值问题整体解的衰减
3.
We discuss the following nonlinear hyperbolic equationu tt -a 1△u-a 2∑ni=1x i(|u x i | m-1 u x i )-a 3△u t=0with the initial boundary value problem, we give the condition of existence and nonexistence for the global solution and the energy decay.
讨论了一类非线性双曲方程utt-a1△u-a2 ∑ni=1 xi(|uxi|m - 1uxi) -a3 △ut =0的初边值问题整体弱解的存在性与不存在性和指数衰减 。
补充资料:双曲线
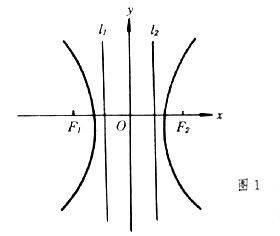
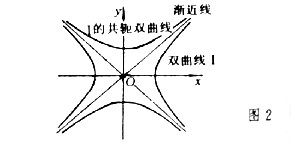
| 双曲线 hyperbola 二次曲线的一种。平面上到两个定点F1、F2的距离之差的绝对值等于一个常数2a的动点的轨迹。定点F1、F2称为双曲线的焦点,两焦点间的距离称为焦距(记为2c)。这个双曲线的标准方程为 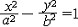 (此处b2=c2-a2)。双曲线有两条互相垂直的对称轴,焦点所在的轴称为实轴,和双曲线不交的轴称为虚轴,分别如图1中的x轴和y轴 。双曲线分为两支,分别位于虚轴的两侧(图1)。标图1准方程中的a,b分别称为双曲线的半实轴长和半虚轴长,a,b相等时,称为等轴双曲线。双曲线有一个对称中心,称为中心,如图1中的坐标原点。双曲线上的动点沿双曲线移向无穷远时,与过中心的两条定直线 (此处b2=c2-a2)。双曲线有两条互相垂直的对称轴,焦点所在的轴称为实轴,和双曲线不交的轴称为虚轴,分别如图1中的x轴和y轴 。双曲线分为两支,分别位于虚轴的两侧(图1)。标图1准方程中的a,b分别称为双曲线的半实轴长和半虚轴长,a,b相等时,称为等轴双曲线。双曲线有一个对称中心,称为中心,如图1中的坐标原点。双曲线上的动点沿双曲线移向无穷远时,与过中心的两条定直线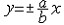 无限接近 ,即距离趋向于零,这两条定直线称为双曲线的渐近线 (图2)。交换双曲线的实轴和虚轴所得的双曲线 无限接近 ,即距离趋向于零,这两条定直线称为双曲线的渐近线 (图2)。交换双曲线的实轴和虚轴所得的双曲线 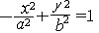 ,称为原来双曲线的共轭双曲线。双曲线和它的共轭双曲线有共同的渐近线(图2)。 双曲线的焦距与实轴长之比 ,称为原来双曲线的共轭双曲线。双曲线和它的共轭双曲线有共同的渐近线(图2)。 双曲线的焦距与实轴长之比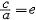 称为双曲线的离心率 。双曲线的离心率大于1,当离心率由小变大时,双曲线开口就由扁狭变得开阔。双曲线也可看成是平面上到定点(焦点)与到定直线(准线)的距离之比(离心率)等于某一大于1的常数的动点的轨迹。双曲线有两条准线(图1),对于焦点F1,相应的准线是l1 ,对于焦点F2,相应的准线是l2 称为双曲线的离心率 。双曲线的离心率大于1,当离心率由小变大时,双曲线开口就由扁狭变得开阔。双曲线也可看成是平面上到定点(焦点)与到定直线(准线)的距离之比(离心率)等于某一大于1的常数的动点的轨迹。双曲线有两条准线(图1),对于焦点F1,相应的准线是l1 ,对于焦点F2,相应的准线是l2
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条