1) three-dimensional fractal dimension
三维分形维数
1.
The three-dimensional fractal dimensions of Fe flocs with more compact structure ranged from 2.
结果表明,质量-粒径法得到的铁盐絮体三维分形维数为2。
2) Three-dimensional fractal information dimension
三维分形信息维数
4) fractal dimension
分形维数
1.
Study on dosage control by flocs fractal dimension;
絮凝体分形维数投药控制研究
2.
Determination of fractal dimensions of silicon dioxide xerogel by means of gas-adsorption;
气体吸附法测定二氧化硅干凝胶的分形维数
3.
Study of fractal dimension and its effect on specific heat capacity of coal or chars;
煤焦分形维数及其对比热容的影响研究
5) fractal dimensions
分形维数
1.
Relation between compressive strength and fractal dimensions of jointed rock-mass;
节理岩体分形维数与抗压强度的关系探讨
2.
Dynamic change of particle size and fractal dimensions of polyferric chloride-humic acid (PFC-HA) flocs;
聚合氯化铁-腐殖酸(PFC-HA)絮体的粒度和分形维数的动态变化
3.
Properties of fractal dimensions of albic soil for radix ginseng culture;
白浆土型人参栽培床土的分形维数特征
6) fractional dimension
分形维数
1.
The fractional dimension of crack section was measured and analyzed.
研究了经硅烷偶联剂处理碳纤维填充增强HPVC板材的力学性能,测量、分析了拉伸断裂面的分形维数,详细论述了数盒子法计算分形维数的原理和计算机的模拟过程。
2.
The fractional characteristics of granularity distribution for sinter of Tangshan stainless steel corporation with different basicity were investigated by fractional theory and their fractional dimensions were worked out by calculation.
文章探讨了在不同碱度条件下烧结矿粒度分布的分形特征,并计算出其粒度组成的分形维数值。
3.
The spatial distributions of porosity and fractional dimension of autotrophic and heterotrophic/autotrophic biofilms applied by direct current in the range of 0～25 A/m 2 were investigated by using the micro slicing technique and image analysis.
采用微切片结合图象分析技术研究外电流 (≤ 2 5A/m2 )对自养、异养 /自养生物膜空隙率和分形维数的影响 。
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 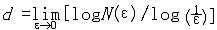 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条