1) fractal box dimension
分形盒维数
1.
A method of automobile license plate based on fractal box dimension and projection is presented.
提出了一种基于分形盒维数与投影法的汽车牌照定位的方法,通过计算分形盒维数搜索到包含车牌的矩形区域,然后对此区域二值化,最后使用投影法精确得到其中车牌的边界坐标,从而将车牌完全从背景中分割出来。
2) box-counting dimensions
分形记盒维数
1.
The classical threshold method is improved, and the endpoint detection algorithm based on the box-counting dimensions and short-time energy-zero-ratio is employed.
文中将分形理论中的分形记盒维数应用到端点检测算法中,采用了基于分形记盒维数与短时能零比相结合的端点检测算法,以分形记盒维数为主要判决条件,并在判决门限的设定上采用了自适应机制。
3) box dimension of fractals
分形盒维
1.
Two parameters,information entropy and box dimension of fractals,are extracted from Hao s graphical representation of DNA sequences.
在DNA序列郝柏林图形化表示方法的基础上,提取出表征图形特征的两个量化参数:信息熵和分形盒维。
4) fractional box-counting dimension
分数盒维数
1.
An original image is divided into non-overlapped blocks,fractional box-counting dimension is used to analyze the feature of the image blocks to extract the feature blocks and secondary feature blocks and then used one level DWT to decompose them.
该算法选用有意义二值图像为水印,把宿主图像分成互不重叠的图像块,用分数盒维数分析各块的特征,提取特征块和次特征块,对它们分别进行一级小波分解,先将水印以不同强度自适应地嵌入到特征块的小波域低频子图中,在保证隐蔽性的前提下,再次将水印以不同强度自适应地嵌入到次特征块的小波域低频子图中,该算法较好地实现了水印的隐蔽性和稳健性。
2.
This paper thus proposed a fast fractal encoding algorithm based on fractional box-counting dimension of an image block,which can find out the best-matched block for an input range block with a reduced search.
针对这个问题,提出了一种快速分形编码算法,它基于图像块的分数盒维数特征,能够在较小的搜索范围内完成输入子块的最佳匹配。
3.
This paper proposes an accelerating scheme based on the categories of fractional box-counting dimension,by discussing their relation between the texture feature of image blocks and fractional box-counting dimension.
针对这个问题,通过分析图像子块的纹理特征与分数盒维数的关系,提出一个基于分数盒维数分类的快速编码算法。
5) fractal box dimension
分形盒子维
1.
Vehicle location and identification method based on fractal box dimensionality;
基于分形盒子维数的车辆定位和识别方法
6) differential box counting
差分盒维数
补充资料：分形维数
| 分形维数 fractal dimension 描述分形最主要的参量。简称分维。通常欧几里德几何中，直线或曲线是1维的，平面或球面是2维的，具有长、宽、高的形体是 3 维的；然而对于分形如海岸线、科赫曲线、射尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述。科赫曲线第一次变换将1英尺的每边换成4个各长4英寸的线段，总长度变为 3×4／3＝4 英尺；每一次变换使总长度变为乘以4／3，如此无限延续下去，曲线本身将是无限长的。这是一条连续的回线，永远不会自我相交，回线所围的面积是有限的，它小于一个外接圆的面积。因此科赫曲线以它无限长度挤在有限的面积之内，确实是占有空间的 ，它比1维要多，但不及2维图形，也就是说它的维数在1和2之间，维数是分数。同样，谢尔宾斯基海绵内部全是大大小小的空洞，表面积是无限大，而占有的 3 维空间是有限的，其维数在2和3之间。 计算分形维数的公式是 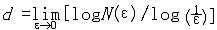 ，式中ε是小立方体一边的长度， N （ε）是用此小立方体覆盖被测形体所得的数目，维数公式意味着通过用边长为ε的小立方体覆盖被测形体来确定形体的维数。对于通常的规则物体 ，覆盖一根单位 长度的线 段所需 的数目要 N （ε）＝1／ε2，覆盖一个单位边长的正方形，N(ε)＝（1／ε）2 ，覆盖单位边 长的立方体，N （ε）＝（1／ε）3。从这三个式子可见维数公式也适用于通常的维数含义。利用维数公式可算得科赫曲线的维数 d＝1.2618，谢尔宾斯基海绵的维数d＝ 2.7268。对于无规分形，可用不同的近似方法予以计算，也可用一定的适当方法予以测定。分维反映了复杂形体占有空间的有效性，它是复杂形体不规则性的量度。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条