1) relaxation of power series


幂级数松弛
2) Poisson exponential series


泊松变幂级数
3) relaxation parameter


松弛参数
1.
In this article we study the relaxation parameter s selection in the Landweber s block-iterative algorithms.
本文将针对Landweber分块迭代算法中松弛参数的选取进行研究。
4) Relaxation function


松弛函数
1.
According to the strain energy density function for finite deformation of viscoelastic material,the relaxation function of Maxwell mode and the deformation gradient tensor of bubble,a stress equation for finite deformation of protein bubble is derived.
根据粘弹性材料有限变形的应变能密度函数、Maxwell模型的松弛函数及气泡的变形梯度张量,推导出蛋白质气泡有限变形的应力方程。
2.
obtaining the stress relaxation data and curves of the Aorta Ascendens under the situation of constant stress and strain,Through regressing analysis the reduced stress relaxation function k(λt)=G(t)T(e)(λ) that we obtain from experiments.
根据冯元桢教授的准线性理论得出肾主动脉松弛函数k(λ,t)=G(t)T(e)(λ)的表达式。
5) relaxation coefficient


松弛系数
1.
In this paper,based on linear creep assumption,(1) tWo theorems about creepcoefficient C(t)and relaxation coefficient K_p(t,)are dirived, i.
本文在线性徐变条件下,(1)导出了关于徐变度和松弛系数的两个定理;(2)提出了直接由徐变度求松弛系数的一种递推公式;(3)对求解徐变问题的初应变法和初应力法,导出了对于任意的松弛系数和徐变度表达式的一般递推公式,从而简化了计算方法,避免了应变或应力历史资料的存贮,节省计算机的大量存贮量。
2.
This new method introduces element s relaxation coefficient,which relates to the working distance and initial ground stress,and it improves conventional finite-element method.
为了克服这一问题,本文引入与开挖面距离和初始地应力有关的单元材料参数松弛系数,对传统有限元方法进行改进,并将其应用于溪洛渡水电站地下厂房开挖与支护的变形监测反馈分析中。
3.
Section 2 explains that the relaxation coefficients A and B,which are related to the shape of the hole and the drilling increment of the multi-layered ceramic coatings,are calculated with eq.
以典型的复合层状材料热障涂层为例,利用有限元分析软件对热障涂层的松弛系数进行了数值计算分析研究。
6) relaxation number


松弛数
1.
The distortional character of crust and mantle medium is judged by relaxation number, the dynamic reason is given to interpreting the strong earthquake activity te.
通过松弛数判断壳幔介质的变形属性,给出印缅板块强震活动趋势的动力学解释。
补充资料:幂级数
| 幂级数 power series 一个无穷阶的多项式。又称为泰勒级数。它的一般形式是a0+a1(z-z0)+…+an(z-z0)n+…=  ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。 ak(z-z0)k ,其中系数ak ,z0及变量z均可取复数值 ,幂级数的收敛域是一个圆盘 ,它可能收缩退化为一个点z=z0 ,也可能扩张为整个复平面,当圆盘有界时,则幂级数在此圆盘的闭面之外一定发散,而在圆盘的边界上,幂级数的和函数至少有一个奇点,即这一点任意一个领域都不能成原来的收敛圆盘的解析开拓圆盘(见解析函数)。将收敛圆盘的半径称为幂级数的收敛半径。有一种幂级数 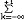 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有 ak(z-z0)k 可能在一个圆的外部 :|z-z0|>r收敛,若同时还有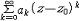 在圆|z-z0|<R上收敛,且 r<R,则级数 在圆|z-z0|<R上收敛,且 r<R,则级数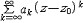 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形 就在圆环 r<|z-z0|<R上收敛,这样的幂级数称为罗朗级数,其中的负幂部分称为它的主要部分,而余下的部分称为解析部分,当一个收敛的罗朗级数的收敛圆环的内圆收缩退化为一个点时,这个点称为罗朗级数和函数(这是一个解析函数)的孤立奇点,若罗朗级数的主要部分为零,则称这一奇点为可去奇点,若主要部分有有限多项,则称该点为和函数的本性奇点,若主要部分因有无限多项 ,则称其为本性奇点 。 一种特殊情形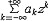 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 在|z|>R收敛于 f(z),则称它为 f(z) 在∞点的罗朗级数,这时称它的正幂部分为主要部分,而其余的部分为解析部分。同样,当主要部分仅有有限多项时,称∞为该级数和函数的极点,当主要部分有无限多项时,称∞为本性奇点。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条