1) infinite Grassmann manifold


无限格拉斯曼流形
2) real Grassmann manifold


实格拉斯曼流形
3) Grassmanian variety


格拉斯曼簇
4) Hermann Günther Grassmann (1809~1877)


格拉斯曼,H.G.
5) Grassmann algebra


格拉斯曼代数
6) Rrassmann space


格拉斯曼空间
1.
That m potential visit points belong to Rrassmann space is proved.


由存储时间优先的出库策略确定了m个可能的访问点,由随机存储策略得到了这m个可能的访问点分别具有的的流通率,证明了这m个可能的访问点属于格拉斯曼空间。
补充资料:格拉斯曼
| 格拉斯曼(1809~1877) Grassmann,Hermann G 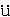 nther nther德国数学家,语言学家,社会活动家。1809年4月15日生于普鲁士波美拉尼亚省的海港城市斯德丁(今什切青,属波兰),1877年9月26日卒于同地。早年曾在柏林大学研习神学、古典语言文学,1830年开始研究数学和物理学。1832年提出一种新的几何理论,从而使J.-L.拉格朗日的《分析力学》(1788)一书的数学论证得到简化,并对P.-S.拉普拉斯的《天体力学》中有关潮汐的部分给以独特的推导。他建立了格拉斯曼代数和格拉斯曼流形的结构,以及在现代分析和微分几何中占据重要地位的外微分形式的计算,此外,还发展了一种“代数乘法”的运算,从而产生了现在称为多项式环的结构。这些成就对后来的数学发展有重大影响,然而却超出了当时数学家们的接受能力,直到他逝世前后才受到重视,并得到应用。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条