1) elliptic trochoidal wave


椭圆余摆线波
2) elliptic trochoid


椭圆摆线
3) cnoidal wave


椭圆余弦波
1.
Considering the nonlinear feature of wave in shallow waters,the cnoidal wave theory is used to calculate the wave force for submarine slope stability.
针对浅水区波浪的非线性特性,提出了在海底边坡稳定性分析中应用椭圆余弦波理论来研究波浪力的问题,利用非线性弥散关系建立了新的适用于整个水深范围的椭圆余弦波的近似求解方法。
2.
The velocities in the oscillatory boundary layer due to linear and cnoidal waves are simulated based on the incompressible D2Q9 model of the Lattice Boltzmann Method.
将波浪作用下的振荡边界层问题化为振动平板边界层问题,利用格子Boltzm ann方法中不可压缩的模型模拟了线性波和椭圆余弦波作用下的层流边界层流速变化,并和理论解进行了比较。
3.
The problems of diffraction on porous multiple vertical cylinders by nonlinear water waves,such as cnoidal wave,solitary wave and second order Stokes wave,are analyzed.
分析了椭圆余弦波、孤立波以及STOKES二阶波对可渗透圆柱群结构的波绕射问题,给出了各类波对结构的绕射势解及STOKES二阶波对结构绕射作用的积分解式。
4) cnoidal waves


椭圆余弦波
1.
Numerical solutions of the equations with the internal generation of sinusoidal and cnoidal waves confirm this finding.
域内生成正弦波和椭圆余弦波的数值试验结果证实了该结论。
2.
The bottom boundary layer under cnoidal waves was studied by using Acoustic Doppler Velocimeter(ADV) technique in a laboratory flume.
通过波浪水槽试验,利用ADV测量椭圆余弦波作用下不同底床情况,垂线上各点的瞬时流速。
3.
It is well know that the Boussinesq equations, which govern the fluid motion in shallow-waters of constant depth, have analytical solutions of both cnoidal waves and solitary waves.
众所周知,该方程有行进波解(孤立波及椭圆余弦波)。
5) trochoidal wave


余摆线波
6) cnoidal wave-typed solution


类椭圆余弦波解
补充资料:椭圆
| 椭圆 ellipse 二次曲线的一种。平面上到两个定点F1,F2的距离之和等于常数2a的动点的轨迹。这两个定点F1,F2称为椭圆的焦点,两焦点间的距离称为焦距(记为2c)。这个椭圆的标准方程为 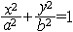 (此外b2=a2-c2) 。椭圆有两条互相垂直的对称轴,焦点所在的轴称为长轴,另一条轴称为短轴,分别如图1中的x轴和y轴。标准方程中的a,b分别称为该椭圆的半长轴长及半短轴长,椭圆有一个对称中心,称为椭圆的中心,如图1中的坐标原点。椭圆的长轴长与焦距之比 (此外b2=a2-c2) 。椭圆有两条互相垂直的对称轴,焦点所在的轴称为长轴,另一条轴称为短轴,分别如图1中的x轴和y轴。标准方程中的a,b分别称为该椭圆的半长轴长及半短轴长,椭圆有一个对称中心,称为椭圆的中心,如图1中的坐标原点。椭圆的长轴长与焦距之比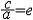 称为椭圆的离心率,因为a>c>0,所以0<e<1。离心率越接近1,椭圆越扁,离心率越接近0,椭圆越接近圆,当两个焦点重合时,椭圆变成圆。还可以把上述椭圆看成是到一个定点与到一条定直线的距离的比等于常数 称为椭圆的离心率,因为a>c>0,所以0<e<1。离心率越接近1,椭圆越扁,离心率越接近0,椭圆越接近圆,当两个焦点重合时,椭圆变成圆。还可以把上述椭圆看成是到一个定点与到一条定直线的距离的比等于常数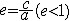 的动点的轨迹,定点是椭圆的焦点,定直线称为椭圆的准线,常数e是椭圆的离心率。椭圆有两条准线(图1),相应于焦点F2的准线是l2,相应于焦点F1的准线是l1,地球绕太阳运行的轨道,就是一个椭圆,太阳位于椭圆的一个焦点上(图2)。人造地球卫星运行的轨道通常也是椭圆,地球的中心是它的一个焦点。 的动点的轨迹,定点是椭圆的焦点,定直线称为椭圆的准线,常数e是椭圆的离心率。椭圆有两条准线(图1),相应于焦点F2的准线是l2,相应于焦点F1的准线是l1,地球绕太阳运行的轨道,就是一个椭圆,太阳位于椭圆的一个焦点上(图2)。人造地球卫星运行的轨道通常也是椭圆,地球的中心是它的一个焦点。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条