1) potency of an ordinal number
序数的基数
2) cardinal numbers and ordinals
基数与序数
3) radix sorting
基数排序
1.
The positive region based on radix sorting is used to get the positive region condition attributes set of decision attributes and the condition attribute set which excludes one of the condition attributes of decision attribute positive region.
采用基数排序思想计算正区域,分别得到决策属性正区域的条件属性集和除决策属性正区域的一个条件属性之外的条件属性集,并且计算这2种属性集的基数之差,以判断该条件属性是否是核属性,依次判断所有条件属性,从而快速获得所需要的核。
2.
By profound exploration on radix sorting algorithm and using of its ideas as “distribution” and “collection”, together with the binary data s feature——Bit Sectional Sorting, a kind of non-comparative sorting algorithm has been developed.
利用基数排序算法“分配”、“收集”的思想 ,以及二进制数据按位存贮的特征 ,改进出一种非比较排序算法———按位分段排序算法 ,并通过对该算法时间复杂度和空间复杂度的分析 ,体现其明显的优越
3.
Correctness of a classic sorting algorithm of linear time complexity and realization of radix sorting were proved and the time complexity of it was analyzed from the viewpoint of the "big-O notation".
采用“大O表示法”客观地分析了基数排序算法的时间复杂度,给出了基数排序算法的实现和正确性的证明,并与比较排序算法作了横向的运行时间的对比。
4) radix sort
基数排序
1.
The essay analyzes the marshalling requirement of shunting plan for train detaching and attaching,and puts forward the problem of shunting trip plan could be solved by using radix sort algorithm,so the shunting mathematicization could be reached,and the sort based on trainset serial had been realized on the CIPS of Chengdu Norther marshalling station.
分析摘挂列车调车计划的编制要求,把调车钩计划的问题应用基数排序算法进行解决,使调车问题数学化,采用按车组序列化排序,并实际应用在成都北编组站综合集成自动化系统(CIPS)中。
2.
In this paper,radix sort using distributing counting sort method is put forward.
提出了一种基于分布计数的基数排序方法,给出该算法定义、算法描述、算法正确性证明和算法分析;讨论了基于该排序算法几个关键问题的解决方法。
3.
A new practical "in-place" sorting algorithm,called super quick sort,is obtained by merging some characteristics of radix sort and quick sort.
快速排序算法结构简单,平均性能较佳;基数排序性能较稳定。
5) base sorting
基数排序
1.
Based on study of base sorting,a new base sorting algorithm is proposed.
基于基数排序的新排序方法,通过对关键字的低半部和高半部做两次基数排序,快速实现排序功能。
2.
In this paper, based on study of base sorting and its language implementing technology,a new base sorting algorithm is proposed .
在把对基数排序算法的研究与对排序算法的语言实现技术的研究相结合起来的基础上提出了一种新的高效基数排序算法 ,给出了该算法的描述 。
6) bases of countable order
可数序基
1.
In this paper, we prove the selection theorems of set valued mappings with valus in the space having bases of countable order, two famous results are improved.
本文利用可数序基的概念，讨论了下半连续集值映射的选择问题，改进了选择理论中的两个经典结论。
补充资料：序数
| 序数 ordinaln umber 集合论的基本概念之一，用来编序的自然数第一、第二、…等的推广。序数概念是G.康托尔首先提出来的。设A是一个非空集。如果在A上建立了一个关系≤，满足①对每个x∈4，有x≤x（自反性）。②x≤y与y≤x蕴涵x＝y（反对称性）。③x≤y与y≤z蕴涵x≤z（传递性）。④对任何x∈A，y∈A，x≤y或y≤x中必有一成立，则称A为全序集。设E是全序集A的一个子集，如果E的元素a满足：对一切x∈E，有a≤x，则称a为E的最小元。如果全序集A的任一非空子集都有最小元，则称A为良序集。例如自然数集在通常≤关系下是良12序集。康托尔把序数定义为良序集的序型。如果两个良序集A和B的元素之间能够建立一一对应，并使A中一前一后的任意两个元素所对应的两个元素，在B中仍保持前后顺序不变，则这样的两个良序集就称为相似集，利用相似关系将良序集分类，凡相似的良序集划入一类。一个这样的相似集的类就称为良序集的一个序型。序型描述了一类集合构造上的共性。例如，所有单元素集互相相似，合为一类，序型相同，所有双元素集互相相似，合为一类，序型也相同，如此等等，所有可数集都可良序化，从而与自然数集 N 有相同的序型。由此可知，序数是同类良序集构造上的共性的抽象 。用0表示空集 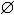 的序数，1表示单元素集的序数，等等，就可以一个接一个地将序数排列起来。用ω表示自然数集N的序数。在序数之间再给出大小关系定义，规定加法和乘法，那么将所有序数从小到大排起来，就形成一个无穷序列：0，1，2,…,ω,ω+1,ω+2,…,ω+ω =ω·2,ω·2+1,…,ω·3,…,ω·ω =ω2,ω2+1,…,ω3,ω3+1,…,ωω,ωω+1,…,…ωωω,…。 1904年E.F.F.策梅洛证明了任一集合都可以良序化 ，以后，说明了任一基数等同于一个序数。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条