1) ordinal
[英]['ɔ:dɪnl] [美]['ɔrdṇəl]
顺序的;序数
2) ordinal
[英]['ɔ:dɪnl] [美]['ɔrdṇəl]
①顺序的 ②序数
3) ordinal
[英]['ɔ:dɪnl] [美]['ɔrdṇəl]
(1)顺序的(2)序数
4) ordinal
[英]['ɔ:dɪnl] [美]['ɔrdṇəl]
序数，顺序的，依次的
5) sequence of unascertained numbers
未确知数的顺序
6) sequential allocation of array
数组的顺序分配
补充资料：序数
| 序数 ordinaln umber 集合论的基本概念之一，用来编序的自然数第一、第二、…等的推广。序数概念是G.康托尔首先提出来的。设A是一个非空集。如果在A上建立了一个关系≤，满足①对每个x∈4，有x≤x（自反性）。②x≤y与y≤x蕴涵x＝y（反对称性）。③x≤y与y≤z蕴涵x≤z（传递性）。④对任何x∈A，y∈A，x≤y或y≤x中必有一成立，则称A为全序集。设E是全序集A的一个子集，如果E的元素a满足：对一切x∈E，有a≤x，则称a为E的最小元。如果全序集A的任一非空子集都有最小元，则称A为良序集。例如自然数集在通常≤关系下是良12序集。康托尔把序数定义为良序集的序型。如果两个良序集A和B的元素之间能够建立一一对应，并使A中一前一后的任意两个元素所对应的两个元素，在B中仍保持前后顺序不变，则这样的两个良序集就称为相似集，利用相似关系将良序集分类，凡相似的良序集划入一类。一个这样的相似集的类就称为良序集的一个序型。序型描述了一类集合构造上的共性。例如，所有单元素集互相相似，合为一类，序型相同，所有双元素集互相相似，合为一类，序型也相同，如此等等，所有可数集都可良序化，从而与自然数集 N 有相同的序型。由此可知，序数是同类良序集构造上的共性的抽象 。用0表示空集 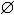 的序数，1表示单元素集的序数，等等，就可以一个接一个地将序数排列起来。用ω表示自然数集N的序数。在序数之间再给出大小关系定义，规定加法和乘法，那么将所有序数从小到大排起来，就形成一个无穷序列：0，1，2,…,ω,ω+1,ω+2,…,ω+ω =ω·2,ω·2+1,…,ω·3,…,ω·ω =ω2,ω2+1,…,ω3,ω3+1,…,ωω,ωω+1,…,…ωωω,…。 1904年E.F.F.策梅洛证明了任一集合都可以良序化 ，以后，说明了任一基数等同于一个序数。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条