1) histogram of binomial distribution


二项分布直方图
3) differential histogram distribution


差分直方图分布
4) Color histogram distribution


颜色直方图分布
5) Histogram distribution


直方图分布特征
6) histogram distribution characteristic


直方图分布特性
补充资料:二项分布
| 二项分布 binomial distribution 概率论中最常用的一种离散型概率分布。若随机变量遵从二项分布,则这个随机变量只取有限个值,即取0,1,2,…,n共n+1个整数值,取k值的概率为 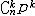 (1-p)n-k(k=0,1,2,…,n; (1-p)n-k(k=0,1,2,…,n;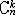 = =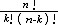 )。记二项分布为B(n,p)。因为 )。记二项分布为B(n,p)。因为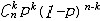 恰好是〔(1-p)+p〕n的二项式展开的第k+1项,所以二项分布由此得名。从不合格率为p的产品中独立地抽取n个产品(每次抽一个,抽取后又放回),其中恰有k个不合格品的概率就是 恰好是〔(1-p)+p〕n的二项式展开的第k+1项,所以二项分布由此得名。从不合格率为p的产品中独立地抽取n个产品(每次抽一个,抽取后又放回),其中恰有k个不合格品的概率就是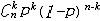 ,所以这n个产品中不合格品数是一个随机变量,它遵从二项分布。类似的例子在生产实践和科学实验中是常见的,将这类问题模型化,假设每一次试验只有两个可能结果:事件A出现或者不出现,A出现的概率为p,不出现的概率为1-p。这种只有两个可能结果的随机试验就称为伯努利试验,将这种试验独立地重复进行n次所组成的随机试验称为n重伯努利试验,其中事件A出现的次数Z是一个服从二项分布B(n,p)的随机变量。二项分布有两个参数n和p,n代表试验的总次数,p代表每次试验事件A出现的概率。二项分布B(n,p)的数学期望为np,方差为np(1-p)。当p固定,n充分大时,二项分布B(n,p)近似于正态分布,当p很小而n较大时,二项分布也可以用泊松分布来近似。 ,所以这n个产品中不合格品数是一个随机变量,它遵从二项分布。类似的例子在生产实践和科学实验中是常见的,将这类问题模型化,假设每一次试验只有两个可能结果:事件A出现或者不出现,A出现的概率为p,不出现的概率为1-p。这种只有两个可能结果的随机试验就称为伯努利试验,将这种试验独立地重复进行n次所组成的随机试验称为n重伯努利试验,其中事件A出现的次数Z是一个服从二项分布B(n,p)的随机变量。二项分布有两个参数n和p,n代表试验的总次数,p代表每次试验事件A出现的概率。二项分布B(n,p)的数学期望为np,方差为np(1-p)。当p固定,n充分大时,二项分布B(n,p)近似于正态分布,当p很小而n较大时,二项分布也可以用泊松分布来近似。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条