1) linear orbital angular momentum


直线型杂化轨函数
2) function of hybridized orbital


杂化轨道函数
3) Trajectory function


轨线函数
6) square hybrid orbital


正方形杂化轨函数
补充资料:杂化轨道
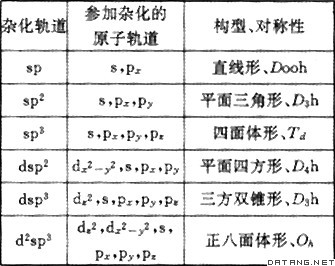
| 杂化轨道 hybrid orbital 一个原子中的几个原子轨道经过再分配而组成的互相等同的轨道。原子在化合成分子的过程中,根据原子的成键要求,在周围原子影响下,将原有的原子轨道进一步线性组合成新的原子轨道。这种在一个原子中不同原子轨道的线性组合,称为原子轨道的杂化。杂化后的原子轨道称为杂化轨道。杂化时,轨道的数目不变,轨道在空间的分布方向和分布情况发生改变。组合所得的杂化轨道一般均和其他原子形成较强的σ键或安排孤对电子,而不会以空的杂化轨道的形式存在。在某个原子的几个杂化轨道中,参与杂化的s、p、d等成分相等,称为等性杂化轨道;若不相等,称为不等性杂化轨道。一些常见的杂化轨道如下表所示:
杂化轨道具有和s,p等原子轨道相同的性质,必须满足正交,归一性。例如,由s和p轨道组成杂化轨道yi=ais+bip,由归一性可得∫yi*yijdt=1,a2+b2=1由正交性可得∫yi*yjdt=0(i 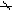 j时)。根据这一性质,考虑杂化轨道的空间分布及未杂化前原子轨道的取向,就能写出各个杂化轨道中原子轨道的组合系数。例如,由s,px ,py组成的平面三角形的sp2杂化轨道y1,y2,y3,当y1极大值方向和x轴平行,由等性杂化概念可知每一轨道s成分占1/3,组合系数为1/ j时)。根据这一性质,考虑杂化轨道的空间分布及未杂化前原子轨道的取向,就能写出各个杂化轨道中原子轨道的组合系数。例如,由s,px ,py组成的平面三角形的sp2杂化轨道y1,y2,y3,当y1极大值方向和x轴平行,由等性杂化概念可知每一轨道s成分占1/3,组合系数为1/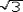 ,其余2/3成分全由p轨道组成,因y1与x轴平行,与y轴垂直,py没有贡献,全部为px,所以得到y1= ,其余2/3成分全由p轨道组成,因y1与x轴平行,与y轴垂直,py没有贡献,全部为px,所以得到y1=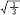 s+ s+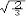 px;同理可得y2= px;同理可得y2=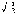 s- s-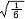 px+ px+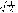 py;y3= py;y3=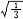 s- s-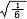 px- px-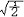 py。并可验证 y1,y2、y3 ,满足正交归一性。根据杂化轨道的正交、归一条件,推求两个等性杂化轨道的最大值之间的夹角θ,可按下式计算:a+βcosθ+ py。并可验证 y1,y2、y3 ,满足正交归一性。根据杂化轨道的正交、归一条件,推求两个等性杂化轨道的最大值之间的夹角θ,可按下式计算:a+βcosθ+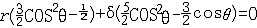 ,式中a,β,γ,δ分别为杂化轨道中s,p,d,f,轨道所占的百分数。两个不等性杂化轨道Ψi和Ψj的最大值之间的夹角θij 可按下式计算: ,式中a,β,γ,δ分别为杂化轨道中s,p,d,f,轨道所占的百分数。两个不等性杂化轨道Ψi和Ψj的最大值之间的夹角θij 可按下式计算: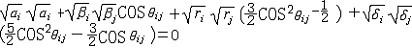 由不等性杂化轨道形成的分子,其准确的几何构型需要通过实验测定,而不能预言其键角的准确值。 由不等性杂化轨道形成的分子,其准确的几何构型需要通过实验测定,而不能预言其键角的准确值。
|
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条