1) interpolation
[英][in,tə:pəu'leiʃən] [美][ɪn,tɚpə'leʃən]


插值/内插
2) interpolation
[英][in,tə:pəu'leiʃən] [美][ɪn,tɚpə'leʃən]


内插值
1.
A new approach for treating curved boundary in Lattice Boltzmann method based on interpolation
格子Boltzmann方法中基于内插值的曲线边界处理新方法
2.
The high vertical resolution is achieved at a larger sampling distance when interpolation algorithm is adopted to reconstruct the 3D profile and the conicoid fitting technique is used to calibrate for the system error in the data processing.
在数据处理上 ,采用了内插值三维重构算法 ,以及二次曲面拟合的系统误差校正算法 ,可以在较大的采样间距下获取较高的测量精度 。
3.
Introduced the structure of BP network,analyzed the principle of prediction with BP network,pointed out that the learning of BP network is fitting of interpolation,discussed the condition of prediction with BP network,and validated it with example.
介绍了BP神经网络的结构,分析了神经网络预测原理,指出神经网络是内插值,讨论了可应用神经网络进行预测的条件,并通过实例进行了验证。
3) interpolation
[英][in,tə:pəu'leiʃən] [美][ɪn,tɚpə'leʃən]


内插值法
1.
In this thesis,the author elaborates the theory of interpolation and brings forth the new ideas in the application of the theory.
对内插值法的基本原理及其在内部收益率和投资回收期决策指标应用方面进行了论述 ,总结出新的计算方法 ,从而简化了这两个指标的计算过
4) intrafield interpolation


场内插值
1.
The proposed method performs specific intrafield interpolation first, and then pixels of the image are classified into four categories by motion detection.
分析了现有的各种去隔行算法,在此基础上,将形态学处理引入基于运动检测的自适应去隔行技术中,对隔行图像进行精确的场内插值,通过运动检测将图像中的像素进行分类,针对不同类型的像素点自适应采取不同的插值算法。
5) numerical interpolation


数值内插
6) right interpolation


右内插值
补充资料:插值
| 插值 interpolation 在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。 早在6世纪,中国的刘焯已将等距二次插值用于天文计算。17世纪之后,I.牛顿,J.-L.拉格朗日分别讨论了等距和非等距的一般插值公式。在近代,插值法仍然是数据处理和编制函数表的常用工具,又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础,许多求解计算公式都是以插值为基础导出的。 插值问题的提法是:假定区间[a,b]上的实值函数f(x)在该区间上 n+1个互不相同点x0,x1……xn 处的值是f [x0],……f(xn),要求估算f(x)在[a,b]中某点 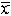 的值。其做法是:在事先选定的一个由简单函数构成的有n+1个参数C0,C1,……Cn的函数类Φ(C0,C1,……Cn)中求出满足条件P(xi)=f(xi)(i=0,1,…… n)的函数P(x),并以P( 的值。其做法是:在事先选定的一个由简单函数构成的有n+1个参数C0,C1,……Cn的函数类Φ(C0,C1,……Cn)中求出满足条件P(xi)=f(xi)(i=0,1,…… n)的函数P(x),并以P(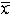 )作为f( )作为f(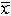 )的估值。此处f(x)称为被插值函数,c0,x1,……xn称为插值结(节)点,Φ(C0,C1,……Cn)称为插值函数类,上面等式称为插值条件,Φ(C0,……Cn)中满足上式的函数称为插值函数,R(x)= f(x)-P(x)称为插值余项。当估算点 )的估值。此处f(x)称为被插值函数,c0,x1,……xn称为插值结(节)点,Φ(C0,C1,……Cn)称为插值函数类,上面等式称为插值条件,Φ(C0,……Cn)中满足上式的函数称为插值函数,R(x)= f(x)-P(x)称为插值余项。当估算点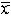 属于包含x0,x1……xn的最小闭区间时,相应的插值称为内插,否则称为外插。 属于包含x0,x1……xn的最小闭区间时,相应的插值称为内插,否则称为外插。多项式插值 这是最常见的一种函数插值。在一般插值问题中,若选取Φ为n次多项式类,由插值条件可以唯一确定一个n次插值多项式满足上述条件。从几何上看可以理解为:已知平面上n+1个不同点,要寻找一条n次多项式曲线通过这些点。插值多项式一般有两种常见的表达形式,一个是拉格朗日插值多项式,另一个是牛顿插值多项式。 埃尔米特插值 对于函数f(x),常常不仅知道它在一些点的函数值,而且还知道它在这些点的导数值。这时的插值函数P(x),自然不仅要求在这些点等于f(x)的函数值,而且要求P(x)的导数在这些点也等于f(x)的导数值。这就是埃尔米特插值问题,也称带导数的插值问题。从几何上看,这种插值要寻求的多项式曲线不仅要通过平面上的已知点组,而且在这些点(或者其中一部分)与原曲线“密切”,即它们有相同的斜率。可见埃尔米特插值多项式比起一般多项式插值有较高的光滑逼近要求。 分段插值与样条插值 为了避免高次插值可能出现的大幅度波动现象,在实际应用中通常采用分段低次插值来提高近似程度,比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数,但它们的总体光滑性较差。为了克服这一缺点,一种全局化的分段插值方法——三次样条插值成为比较理想的工具。见样条函数。 三角函数插值 当被插函数是以2π为周期的函数时,通常用n阶三角多项式作为插值函数,并通过高斯三角插值表出。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条