1) convolution of distributions
广义函数卷积
2) convolution of distributions
广义函数的卷积
3) generalized convolution algebra
广义卷积代数
1.
With the theory of Hun semigroups,we proved that any regular generalized convolution algebra,with the generalized convolution operation and endowed with the weak- ly convergent topology,forms a metrizable,stable and normable Hun semigroup,without non-unity idempotent elements.
利用 Hun 半群理论,证明了任一正则广义卷积代数,按广义卷积运算和弱收敛拓扑构成一个可度量化。
4) generalized convolution
广义卷积
1.
The generalized convolution of probability measures defined on R+=[0,∞) was extended to the compact space =[0,∞]in an alternative way,comparing with that one used by Urbanik.
把定义在半直线 R+=[0,∞)上概率测度的广义卷积推广到了紧空间 +=[0,∞]上。
5) broad integral of positive function
正函数广义积分
6) integration of generalized function
广义函数积分
补充资料：广义函数
| 广义函数 generalized function，distribution 古典函数概念的推广。关于广义函数的研究构成了泛函分析中有着广泛应用的一个重要分支。历史上第一个广义函数是由物理学家P.A.M.狄拉克引进的，他因为陈述量子力学中某些量的关系时需要引入了“函数”δ（x）：当x≠0时，δ（x）＝0，但 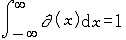 。按20世纪前所形成的数学概念是无法理解这样奇怪的函数的。然而物理学上一切点量，如点质量、点电荷、偶极子、瞬时打击力、瞬时源等物理量用它来描述不仅方便、物理含义清楚，而且当它被当作普通函数参加运算，如对它进行微分和傅里叶变换，将它参与微分方程求解等所得到的数学结论和物理结论是吻合的。这就迫使人们要为这类怪函数确立严格的数学基础。最初理解的方式之一是把这种怪函数设想成直线上某种分布所相应的“密度”函数。所以广义函数又称为分布，广义函数论又称分布理论。用分布的观念为这些怪函数建立基础虽然很直观，但对于复杂情况就又显得繁琐而不很明确。后来随着泛函分析的发展，L.施瓦尔茨（1945）用泛函分析观点为广义函数建立了一整套严格的理论，接着I.M.盖尔范德对广义函数论又作了重要发展。从此，广义函数被广泛地应用于数学、物理、力学以及分析数学的其他各个分支，例如微分方程、随机过程、流形理论等等，它还被应用到群的表示理论，特别是它有力地促进了偏微分方程近30年来的发展。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条