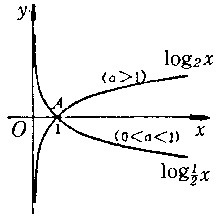1) Function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


功能,职能,函数
2) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


函数,功能,作用,职能
3) function performance


函数功能
1.
Machining discal cam using unmerical control system function performance;


用数控系统的函数功能加工盘形凸轮
4) performance function


功能函数
1.
Based on the structure reliability analysis and results of structural optimization theory,the performance function and computative method of reliability index of the homogeneous truss structure under certain failure mode were derived and given,respectively.
以结构可靠性分析和结构优化理论成果为基础,推导得到匀质杆件结构在特定失效模式下的功能函数,给出这一特定失效模式下结构可靠度指标的计算方法。
2.
Aiming at the deployable joints in truss antenna,considering them as separate rockers,breaking up the function,its movement reliability was found to have two parallel performance functions:the performance function according to deploying work and that according to deploying moment.
将桁架式可展开天线的运动关节简化为单节摇杆,并对摇杆执行功能的过程进行分解,分析指出了其运动功能可靠度中包含矩的功能函数和功的功能函数这两个并联的功能函数。
3.
Structural reliability index for response surface method of RBF ANN was developed,which could resolve the error of structural reliability when the structure performance function was nonlinear or the variables were nonnormally distributed.
提出了逐步逼近径向基神经网络响应面法计算结构可靠度,这种数值方法较好地解决了结构功能函数非线性及结构随机变量非正态分布时采用结构可靠度指标度量结构可靠度存在误差的问题。
5) functional function


功能函数
1.
This method doesn t have to transform the functional function into the independent standard normal space,and need not the calculation as well on the first ordered and second ordered partial derivative of the logarithm of joint-probability density function,therefore this method is suitable for engineering application.
这种方法不必把功能函数变换到独立标准正态空间,也不需要计算联合概率密度函数对数的一阶、二阶偏导数,计算步骤简便且利于编程计算,因此适合于工程应用。
2.
By using functional function equation,the computing formula of failure mode related correlation coefficient and reliability is given on the basis of the theory of O.
利用功能函数方程 ,根据O 。
3.
Starting from the probability theory of fuzzy event,the paper briefly introduced the basic thought about application of fuzzy probability vulcanite, constructed functional function used for identification of vulcanite fuzzy probability.
本文从模糊事件概率理论基础入手,简要介绍了应用模糊概率识别火山岩的基本思路,构建了用于火山岩模糊概率识别功能函数。
6) function
[英]['fʌŋkʃn] [美]['fʌŋkʃən]


功能函数
1.
Derivation for Explicit Function of Asphalt Pavement Structure and Study on Structural Reliability
沥青路面显式功能函数的推导及其可靠度分析
2.
The technical kernel of the system is the multi functional logical operation(MFLO),which is brought about by developing a series of functions,and these functions are based on the properties of natural languages such as linearity,discreteness,recursiveness and hierarchy,etc.
该系统的技术核心是多功能逻辑运算分析技术 ,该技术的实现是靠建立一系列的功能函数 ,而这些功能函数是建立在诸如线性、离散性、递归性、层次性等自然语言的特性的基础之上的。
3.
The functions expressed by moment of flexion or axial force for the bearing capacity of head-on cross-section under typical condition were given in the previous study,but they can not fully attribute the working mode of the duct piece.
以往的研究中给出了典型条件下弯矩表达或轴力表达的正截面承载能力功能函数,但并不能全面表征衬砌管片的工作模式。
补充资料:函数
| 函数 functions 数学中的一种对应关系,是从某集合A到实数集B的对应。简单地说,甲随着乙变,甲就是乙的函数。精确地说,设X是一个不空集合,Y是某个实数集合,f是个规则,若对X中的每个x,按规则f,有Y中的一个y与之对应,就称f是X上的一个函数,记作y=f(x),称X为函数f(x)的定义域,Y为其值域,x叫做自变量,y为因变量。 例1:y=sinx X=[0,2π],Y=[-1,1],它给出了一个函数关系。当然,把Y改为Y1=(a,b),a<b为任意实数,仍然是一个函数关系。 例2:某商场一年12个月毛线的零售量(单位:百千克)变化,见表1。
例3:某河道的一个断面图如图1所示。
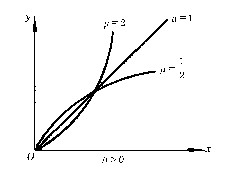
其深度y与一岸边点O到测量点的距离x之间的对应关系呈曲线,这代表一个函数,定义域为[0,b]。以上3例展示了函数的三种表示法:公式法,表格法和图像法。 复合函数 有3个变量,y是u的函数,y=ψ(u),u是x的函数,u=f(x),往往能形成链:y通过中间变量u构成了x的函数: x→u→y,这要看定义域:设ψ的定义域为U。f的值域为U,当U*ÍU时,称f与ψ构成一个复合函数,例如y=lgsinx,x∈(0,π)。此时sinx>0,lgsinx有意义。但如若规定x∈(-π,0),此时sinx<0,lgsinx无意义,就成不了复合函数。 反函数 就关系而言,一般是双向的,函数也如此,设y=f(x)为已知的函数,若对每个y∈Y,有唯一的x∈X,使f(x)=y,这是一个由y找x的过程,即x成了y的函数,记为x=f -1(y)。称f -1为f的反函数。习惯上用x表示自变量,故这个函数仍记为y=f -1(x),例如y=sinx与y=arcsinx互为反函数。在同一坐标系中,y=f(x)与y=f -1(x)的图形关于直线y=x对称。 隐函数 若能由函数方程F(x,y)=0确定y为x的函数y=f(x),即F(x,f(x))≡0,就称y是x的隐函数。 多元函数 设点(x1,x2,…,xn)∈GÍRn,UÍR1,若对每一点(x1,x2,…,xn)∈G,由某规则f有唯一的u∈U与之对应:f:G→U,u=f(x1,x2,…,xn),则称f为一个n元函数,G为定义域,U为值域。 基本初等函数及其图像 幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。 ①幂函数:y=xμ(μ≠0,μ为任意实数)定义域:μ为正整数时为(-∞,+∞),μ为负整数时是(-∞,0)∪(0,+∞);μ= 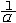 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为 (α为整数),当α是奇数时为(-∞,+∞),当α是偶数时为(0,+∞);μ=p/q,p,q互素,作为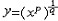 的复合函数进行讨论。略图如图2、图3。 的复合函数进行讨论。略图如图2、图3。
②指数函数:y=ax(a>0,a≠1),定义成为(-∞,+∞),值域为(0,+∞),a>0时是严格单调增加的函数(即当x2>x1时, 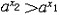 ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=( ),0<a<1时是严格单减函数。对任何a,图像均过点(0,1),注意y=ax和y=(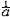 )x的图形关于y轴对称。如图4。 )x的图形关于y轴对称。如图4。
③对数函数:y=logax(a>0),称a为底,定义域为(0,+∞),值域为(-∞,+∞)。a>1时是严格单调增加的,0<a<1时是严格单减的。不论a为何值,对数函数的图形均过点(1,0),对数函数与指数函数互为反函数。如图5。
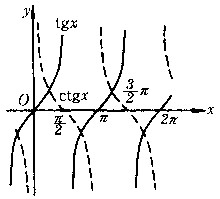
④三角函数:见表2。
正弦函数、余弦函数如图6,图7所示。
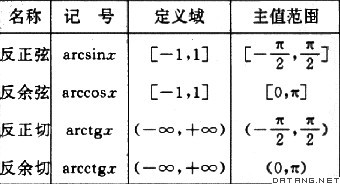
⑤反三角函数:见表3。双曲正、余弦如图8。
⑥双曲函数:双曲正弦 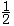 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 (ex-e-x),双曲余弦(ex+e-x),双曲正切(ex-e-x)/(ex+e-x),双曲余切(ex+e-x)/(ex-e-x)。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条