1) Fresnal diffraction string
费涅尔衍射条纹
2) Fresnel difraction
费涅耳衍射
1.
By adding quadratic phase factor to the Fourier s Kinoform, we derive a new Fresnel s Kinoform whose object can be reconstructed in the Fresnel difraction field.
利用对称性进了两维快速傅里叶变换（ＦＦＴ），以这种改进的快速傅里叶变换模拟相干光的费涅耳衍射，设计出傅里叶型Ｋｉｎｏｆｏｒｍ和等效于透镜的 Ｋｉｎｏｆｏｒｍ合二为一的费涅耳型 Ｋｉｎｏｆｏｒｍ。
3) Fresnel diffraction
菲涅尔衍射
1.
A method for calculating return waveform was deduced by the theory of Fresnel diffraction,and the models of return waveform from ground of slope,ladder and vegetation terrains were estibalished.
利用菲涅尔衍射理论推导出高斯型激光脉冲的回波计算方法,建立了斜坡、阶梯和植被三种标准漫反射地物的回波模型,以GLAS(Geoscience Laser Altimeter System)系统为例,通过数值计算得到了标准漫反射地物的回波信号波形,分析了回波波形与三种地物模型参数、光束扫描角之间的关系。
2.
This paper discusses the relationship between the fractional Fourier transform and the Fresnel diffraction, and presents that the optical diffraction from a spherical surface equals the scaled fractional Fourier transform.
讨论了分数傅里叶变换与菲涅尔衍射的关系,提出球面衍射过程就是一种具有尺度因子的分数傅里叶变换,并应用分数傅里叶变换进行衍射光学元件的设计。
3.
This study focus on light intense arrangements of Fraunbofer and Fresnel diffraction, found that both dark stripes are located on same positions, so that diffraction measur.
通过对菲涅尔衍射和夫琅和费衍射光强分布的深入研究，发现二者暗纹分布是相同的。
4) Diffraction Stripe
衍射条纹
1.
Data Processing of Diffraction Stripes During CCD Measurement;
CCD检测衍射条纹的数据处理
5) diffractive stripe
衍射条纹
1.
The distribution rule of the diffractive stripe and diffractive intensity are given,which are accord with the experimental results.
表明衍射条纹的方位由相位光栅方程决定,衍射条纹的强度由相应阶次的J2m(v)函数值决定。
2.
The diffractive stripe azimuth of acoustic traveling wave and acoustic standing wave are determined by the same diffractive equation, and the intensity of diffractive stripe is determined by the value of J2m(v).
讨论了液体介质中的超声相位光栅的形成,根据声光相互作用类型的区分标准,在液体介质的超声光栅实验中声光相互作用一般为Naman-Nath衍射;相位光栅可以由声行波和声驻波形成,且形成的各级衍射条纹极大均由相同的光栅方程决定,各级衍射条纹的强度由相应阶次的J2m(v)函数值决定;在此基础上给出了衍射条纹和衍射光强的分布特点。
6) round-hole Fresnel diffraction
圆孔菲涅尔衍射
补充资料：菲涅耳衍射
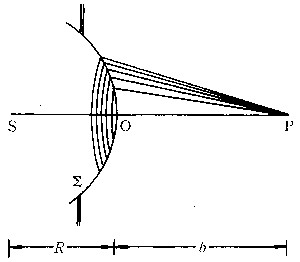
| 菲涅耳衍射 Fresnel diffraction 光源和观察屏离障碍物（孔或屏）为有限远时的衍射 。以单色点光源照射圆孔，在有限远处设置观察屏，在屏上将观察不到圆孔的清晰几何影，而是一组明暗交替的同心圆环状衍射条纹。以不透光的圆屏代替圆孔，在原几何影中心可观察到亮点，外围与圆孔衍射一样是明暗交替的圆环条纹 。以上是菲涅耳衍射的典型例子。根据惠更斯-菲涅耳原理计算菲涅耳衍射的强度分布时，必须对波前作无限分割，然后用积分求次波的合振幅，计算比较复杂。在处理圆孔或圆屏衍射时常用菲涅耳半波带法，它是用较粗糙的分割来代替对波前的无限分割，相应地，次波叠加时的积分可简化成多项式求和。此法虽然不够精确，但可较方便地得出菲涅耳衍射的主要特征。 菲涅耳圆孔衍射 如图1，S是波长为λ的点光源，P为观察点。考虑半径为R的球面波前Σ，它与SP交于O点。以观察点P为中心，依次以 b＋λ／2，b＋λ，b＋3λ／2，b＋2λ，……为半径作一系列球面，把Σ分割成许多以O为心的圆环带。每个环带看成是发射次波的一个单元，相邻两环带所发次波到达P点的光程差（见光程）均为λ／2（对应相位差为π），故每个环带称为半波带。从中心O算起，设第k个半波带在P点引起的振幅为ak，则有akαFΔSk／rk ，式中ΔSk为第k个波带的面积，rk为它到P点的距离，F为该波带处的倾斜因子。从几何上可证ΔSk／rk近似为常数，故ak仅由倾斜因子决定，按菲涅耳的假设，有a1 ＞a2＞a3＞…。故P点的合振幅为A＝a1－a2＋a3－a4 ＋……
若在波前Σ处放置一带圆孔的无穷大不透光屏，圆孔中心在连线SP上，则P点的合振幅A就由未被遮挡的半波带数决定，A等于有限项之和，其大小由露出的半波带数的奇偶性决定。半波带的划分与观察点P的位置有关，当P点沿轴线移动时，露出的半波带数的奇偶性将交替变化，P点的强度也作明暗交替变化。当观察点向轴外移动时，露出的半波带不断变化，强度也相应地作明暗交替变化，于是形成圆环条纹。 菲涅耳圆屏衍射 以不透光的圆屏代替圆孔(图2)，中央部分的半波带将被挡住，设正好挡掉k个半波带，则P点振幅为： A＝ak+1－ak+2＋ak+3－……＋a∞＝ak+1/2 得圆屏衍射图样的中心点为亮点，周围与圆孔衍射一样是明暗交替的同心圆环条纹。1818年，A.-J.菲涅耳参加了法国科学院主办的一次征文竞赛，发表了关于衍射理论的论文。评审委员会成员之一的S.D.泊松反对光的波动说，他仔细审核了菲涅耳的理论，得出圆屏几何影中心应为亮点的结论（故称泊松亮点），他利用这一当时看来与日常经验相违背的结论对菲涅耳的理论提出异议。但过后不久，D.F.J.阿拉戈在实验中果真发现了几何影中心为亮斑（故又称阿拉戈斑）。这成为菲涅耳的衍射理论和光的波动说取得决定性胜利的标志。
菲涅耳波带片 对特定的观察点可设计一种特殊的遮光屏，把所有奇数或偶数的半波带遮掉，则观察点将是强度大大增强的亮点，如同光源的像点一样，这种特殊遮光屏称为菲涅耳波带片，它与透镜一样具有成像性质，其焦距为 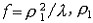 ，ρ1为第一个半波带的半径 ，λ为波长。与透镜不同的是，除上述主焦距外，还有f／3，f／5，f／7，…等次焦距。波带片除有会聚性质外，还有发散性质，即存在－f，－f／3，－f／5，…等一系列虚焦距 。现代波带片的种类很多，除上述振幅型的外，还有相位型；透射率有矩形函数，也有正弦函数；有用于可见光波段，也有用于微波波段，等等。 |
说明：补充资料仅用于学习参考，请勿用于其它任何用途。
参考词条