1) convolution
[英][,kɔnvə'lu:ʃn] [美]['kɑnvə'luʃən]


卷积;旋转;圈,匝
2) convolution
[英][,kɔnvə'lu:ʃn] [美]['kɑnvə'luʃən]


①褶积式 ②匝,圈,转数 ③旋转
3) convolution
[英][,kɔnvə'lu:ʃn] [美]['kɑnvə'luʃən]


盘旋,缠绕,涡流,回旋;匝,圈;卷积
4) turn
[英][tɜ:n] [美][tɝn]


①转动 ②匝,圈
5) multiturn rotary encoder


多匝旋转编码器,多圈回转编码器
6) turn
[英][tɜ:n] [美][tɝn]


圈,匝
补充资料:卷积
| 卷积 convolution 分析数学中一种重要的运算。设f(x), g(x)是R1上的两个可积函数,作积分: 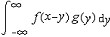 可以证明,关于几乎所有的x∈(-∞,∞) ,上述积分是存在的。这样,随着x的不同取值 ,这个积分就定义了一个新函数h(x),称为f与g的卷积,记为h(x)=(f *g)(x)。容易验证,(f *g)(x)=(g *f)(x),并且(f *g)(x)仍为可积函数。这就是说,把卷积代替乘法,L1(R1)1空间是一个代数,甚至是巴拿赫代数。 可以证明,关于几乎所有的x∈(-∞,∞) ,上述积分是存在的。这样,随着x的不同取值 ,这个积分就定义了一个新函数h(x),称为f与g的卷积,记为h(x)=(f *g)(x)。容易验证,(f *g)(x)=(g *f)(x),并且(f *g)(x)仍为可积函数。这就是说,把卷积代替乘法,L1(R1)1空间是一个代数,甚至是巴拿赫代数。卷积与傅里叶变换有着密切的关系。以 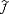 (x) , (x) , (x)表示L1(R)1中f和g的傅里叶变换,那么有如下的关系成立:(f *g)∧(x)= (x)表示L1(R)1中f和g的傅里叶变换,那么有如下的关系成立:(f *g)∧(x)=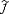 (x)· (x)· (x),即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系,使傅里叶分析中许多问题的处理得到简化。 (x),即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换。这个关系,使傅里叶分析中许多问题的处理得到简化。由卷积得到的函数(f *g)(x),一般要比f,g都光滑。特别当g为具有紧支集的光滑函数,f 为局部可积时,它们的卷积(f *g)(x)也是光滑函数。利用这一性质,对于任意的可积函数 , 都可以简单地构造出一列逼近于f 的光滑函数列fs(x),这种方法称为函数的光滑化或正则化。 卷积的概念还可以推广到数列 、测度以及广义函数上去。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条