1) circle function


圆域函数
2) hyperelliptic function field


超椭圆函数域
3) liptic modular function field


椭圆模函数域
4) elliptic function


椭圆函数
1.
By using the elliptic function and conformal transformation theory,a close form solution to this problem is obtained.
运用椭圆函数和保角变换理论,获得了该问题严格的闭合解。
2.
Phase plane properties of an electron in Wiggler field are analysed by using Jacobian elliptic function and elliptic integral based on the pendulum equation for FEL.
从自由电子激光器的摆方程出发,利用Jacobian椭圆函数和椭圆积分分析了系统的相平面特征,并利用加速器概念和束流动力学方法,讨论了系统的稳定性、增益和临界特征等问题。
3.
A class of new doubly periodic wave solutions for(2+1)-dimensional breaking soliton equation are obtained by introducing appropriate Jacobi elliptic function and Weierstrass elliptic function in the general solution(contains two arbitrary functions)got by means of multilinear variable separation approach for(2+1)-dimensional breaking soliton equation.
在多线性分离变量法所得(2+1)维破裂孤子方程广义解(包含2个任意函数)中引入符合条件的Jacobi椭圆函数和Weierstrass椭圆函数,从而获得了该系统的新双周期解。
5) circular harmonic function


圆谐函数
6) circularity function


圆度函数
1.
A fuzzy arc is given by a simple curve and its circularity function.


一个模糊圆弧由一条简单曲线段和该曲线段的圆度函数共同给出。
补充资料:椭圆函数
| 椭圆函数 elliptic function 在有限复平面上亚纯的双周期函数。所谓双周期函数是指具有两个基本周期的单复变函数,即存在ω1,ω2两个非0复数, 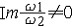 ,而对任意整数n,m,有f(z+nω1+mω2)=f(z) ,于是{nω1+mω2|n,m为整数}构成f(z)的全部周期,在复平面上任取一点a,以a,a+ω1,a+ω1+ω2,a+ω2为顶点的平行四边行的内部 ,再加上两个相邻的边及其交点,这样构成的一个半开的区域称为f(z)的一个基本周期平行四边形,将它平行移动nω1+mω2,当n,m取遍所有整数时,即得一覆盖整个复平面的周期平行四边形网,f(z)在每一个周期平行四边形中的性质都和它在基本周期平行四边形中的一样。在基本周期平行四边形中,f(z)有以下性质:非常数椭圆函数一定有极点,且极点留数之和必为零,因而不可能只有一个一阶极点,有n个极点的椭圆函数称为n阶椭圆函数 ,它在基本周期平行四边形内取任一值n次,即对任意复数A,f(z)-A在基本周期平行四边形内有且仅有n个零点 ,且f(z)的零点之和与极点之和的差必等于一个周期。 ,而对任意整数n,m,有f(z+nω1+mω2)=f(z) ,于是{nω1+mω2|n,m为整数}构成f(z)的全部周期,在复平面上任取一点a,以a,a+ω1,a+ω1+ω2,a+ω2为顶点的平行四边行的内部 ,再加上两个相邻的边及其交点,这样构成的一个半开的区域称为f(z)的一个基本周期平行四边形,将它平行移动nω1+mω2,当n,m取遍所有整数时,即得一覆盖整个复平面的周期平行四边形网,f(z)在每一个周期平行四边形中的性质都和它在基本周期平行四边形中的一样。在基本周期平行四边形中,f(z)有以下性质:非常数椭圆函数一定有极点,且极点留数之和必为零,因而不可能只有一个一阶极点,有n个极点的椭圆函数称为n阶椭圆函数 ,它在基本周期平行四边形内取任一值n次,即对任意复数A,f(z)-A在基本周期平行四边形内有且仅有n个零点 ,且f(z)的零点之和与极点之和的差必等于一个周期。在以上性质的规范下 ,有两大类重要的椭圆函数:①魏尔斯特拉斯-δ函数。它表作 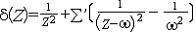 ,其中ω=2nω1+2mω2,Σ'表n,m取遍全部整数之和 ,但要除去ω=0的情形。这是一个二阶椭圆函数,在周期平行四边形中,仅有一个ω是二阶极点,ω=δ(z)满足微分方程(ω′)2=4ω3-g2ω-g3,其中g2=60Σ' ,其中ω=2nω1+2mω2,Σ'表n,m取遍全部整数之和 ,但要除去ω=0的情形。这是一个二阶椭圆函数,在周期平行四边形中,仅有一个ω是二阶极点,ω=δ(z)满足微分方程(ω′)2=4ω3-g2ω-g3,其中g2=60Σ'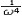 g3=140Σ' g3=140Σ'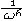 ,由此可见ω=δ(z)是 ,由此可见ω=δ(z)是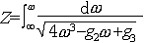 的反函数,右边的积分称为椭圆积分。可以证明,所有的椭圆函数都可以用δ(z)函数来表示 ,而每一个椭圆函数都一定满足一个常系数一阶的代数微分方程。②雅可比椭圆函数。它定义为椭圆积分 的反函数,右边的积分称为椭圆积分。可以证明,所有的椭圆函数都可以用δ(z)函数来表示 ,而每一个椭圆函数都一定满足一个常系数一阶的代数微分方程。②雅可比椭圆函数。它定义为椭圆积分 的反函数 ,记作ω=J(z),J(z)的基本周期平行四边形是一个矩形 ,其基本周期是4K与2iK′,此处 的反函数 ,记作ω=J(z),J(z)的基本周期平行四边形是一个矩形 ,其基本周期是4K与2iK′,此处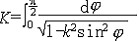 , ,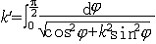 ,其二阶极点为iK′,而k是一个实常数。 ,其二阶极点为iK′,而k是一个实常数。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条