1) underdeterminate system of partial differential equations


欠定偏微分方程组
3) underdetermined system of equations


欠定方程组
4) partial differential equation


偏微分方程组
1.
The paper rewrites the traffic flow macro models in the form of system of quasilinear hyperbolic partial differential equation of first order, and classifies the models in terms of the coefficient in the equation.
将交通流模型表示成拟线性一阶双曲型偏微分方程组;按照方程组中的系数值,对交通流的各种宏观模型进行了分类;依据特征线的特征速度是否小于宏观运动速度,模型是否依赖外来的速度-密度平衡关系以及模型代表的交通流特点等三项指标对模型进行了评价。
2.
Existence and uniqueness of local analytic solution of the partial differential equations |k i| ux k i =A i(x,u,.
把柯西 -柯尔列夫斯卡娅定理推广到如下偏微分方程组 : | ki| u xki =Ai( x,u,… , |α| u xα )( i =1,… ,r, x =( x1 ,… ,xm) ,|α| =α1 +… +αm) 。
6) partial differential equations


偏微分方程组
1.
Hypercomplex function-the popularization of complex function on high dimension,has superiority on solving partial differential equations,which simplifies the process of solving many problems.
并以一个三元高次偏微分方程组和两个电磁场问题求解为例,用提出的方法得到了与经典求解法一致的结果。
2.
Expansion method about the Jacobi elliptic function is firstly applied to systems of nonlinear partial differential equations.
首次将Jacobi椭圆函数展开法应用于求解非线性偏微分方程组,以变异的Boussinesq方程为例演示了方法的有效性,用此方法求出的精确周期解包含了冲击波解。
3.
The idea of soluing is that nonlinear partial differential equations are changed into algebra equations.
通过函数变换,得到了Noyes-Field方程组及Burgers-KdV方程的行波解,求解的基本思路是把非线性偏微分方程组化为代数方程组求解,所用方法具有广泛的实用性。
补充资料:偏微分方程
| 偏微分方程 partial differential equation 含有未知函数及其各阶偏导数的方程。如( 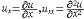 余类此) 余类此)ut-a2(uxx+uyy+uzz)=0(1)其中u=u(x,y,z,t)为未知函数,x,y,z,t是自变量。18世纪,数学家们已开始用偏微分方程来研究问题。方程(1)便是用来描述热的传导规律的。1746年,J.LeR.达朗贝尔给出了一维波动方程(两端固定的弦的振动问题): 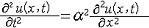 由于弦的两端固定,故在x=0和x=l处(l为弦的长度)应满足边界条件: 由于弦的两端固定,故在x=0和x=l处(l为弦的长度)应满足边界条件:u(0,t)=0 u(l,t)=0 t≥0(3)又当t=0时的状态,即初始条件是 u(0,x)=j(x) ut(0,x)=ψ(x)(4) 一般,每个偏微分方程有许多解,且含有任意函数,一阶方程的解含有一个任意函数,二阶方程的解含有两个任意函数,例如(2)有解u=f(x-at)+g(x+at),其中f(x)、g(η)是二次可微的函数。通常,更注重求满足某些附加条件的特解:未知函数在初始时刻所满足的条件叫初始条件 ,如(4),在所给区域边界上所满足的条件叫边界条件,如(3),初始条件和边界条件统称定解条件,这都要由实际问题来确定。求方程满足初始条件的定解问题叫初值问题或柯西问题,只含边界条件的定解问题叫边值问题,既有初始条件,又有边界条件的问题称为初边值问题或混合问题。如果某个解,当定解条件中的量变化不大时,解的变化也不大,就称解连续依赖于定解条件。若定解问题的解存在、唯一且连续依赖于定解条件,就称定解问题为适定的或称问题的提法是正确的。 |
说明:补充资料仅用于学习参考,请勿用于其它任何用途。
参考词条